Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho tam giác ABC vuông tại A và có BC...
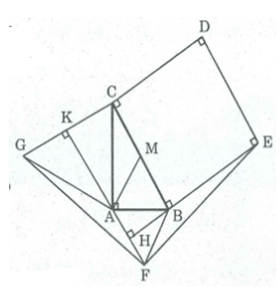
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía
Câu hỏi :
Cho tam giác ABC vuông tại A và có BC = 2AB, AB = a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều AGC. Tính các góc B, C, cạnh AC và diện tích tam giác ABC.
* Đáp án
* Hướng dẫn giải
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra AMB đều ⇒ (ABC) =
Mặt khác: (ABC) + (ACB) = (tính chất tam giác vuông)
Suy ra: (ACB) = - (ABC) = – =
Trong tam giác vuông ABC, theo Pi-ta-go, ta có:
⇒ ⇒ AC = a
Vậy = 1/2 .AB.AC
=
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247