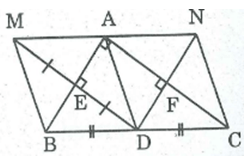
Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC

* Hướng dẫn giải

Tứ giác AEDF là hình chữ nhật

⇒ DE // AC; DF // AB

Trong $∆$ABC, ta có: DB = DC (gt)

Mà DE // AC

Suy ra: AE = EB (tính chất đường trung bình của tam giác)

Lại có: DF // AB và DB = DC

Suy ra: AF = FC (tính chất đường trung bình của tam giác)

Xét tứ giác ADBM, ta có: AE = EB (chứng minh trên)

ED = EM (vì AB là trung trực DM)

Suy ra tứ giác ADBM là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

Mặt khác: AB ⊥ DM

Vậy hình bình hành ADBM là hình thoi (vì có hai đường chéo vuông góc)

Xét tứ giác ADCN, ta có: AF = FC (chứng minh trên)

DF = FN (vì AC là đường trung trực DN)

Suy ra tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

Lại có: AC ⊥ DN

Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)