Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
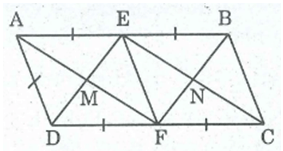
Cho hình bình hành ABCD có AB=2AD. Gọi E và...
Cho hình bình hành ABCD có AB=2AD. Gọi E và F theo thứ tự là trung
Câu hỏi :
Cho hình bình hành ABCD có AB=2AD. Gọi E và F theo thứ tự là trung điểm của AB và CD. Hình bình hành ABCD nói trên có thêm điều kiện gì thì EMFN là hình vuông.
* Đáp án
* Hướng dẫn giải
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ A = ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ A =
Hình thoi AEFD có A = nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247