Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự các điểm
Câu hỏi :
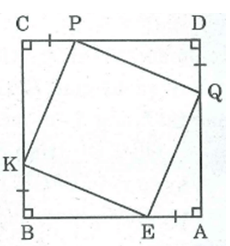
Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì? Vì sao?
* Đáp án
* Hướng dẫn giải
Ta có: AB = BC = CD = DA (gt)
AE = BK = CP = DQ (gt)
Suy ra: EB = KC = PD = QA
* Xét ΔAEQ và ΔBKE,ta có:
AE = BK (gt)
(EAQ) = (KBE) =
QA = EB (chứng minh trên)
Suy ra: AEQ = BKE (c.g.c) ⇒ EQ = EK (1)
* Xét BKEvà CPK,ta có: BK = CP (gt)
(KBE) = (PCK) =
EB = KC ( chứng minh trên)
Suy ra: BKE = CPK (c.g.c) ⇒ EK = KP (2)
* Xét CPK và DQP,ta có: CP = DQ (gt)
C = D =
DP = CK ( chứng minh trên)
Suy ra: CPK = DQP (c.g.c) ⇒ KP = PQ (3)
Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ
Hay tứ giác EKPQ là hình thoi.
Mặt khác: AEQ = BKE
⇒ (AQE) = (BEK)
Mà (AQE) + (AEQ) =
⇒ (BEK) + (AEQ) =
Ta có: (BEK) + (QEK) + (AEQ ) =
Suy ra: (QEK ) = -( (BEK ) + (AEQ) )= - =
Vậy tứ giác EKPQ là hình vuông.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Copyright © 2021 HOCTAP247