Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm
Câu hỏi :
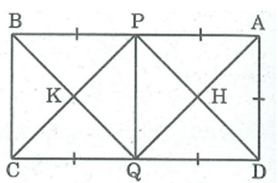
Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.
* Đáp án
* Hướng dẫn giải
* Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD
AP = 1/2 .AB (gt)
QD = 1/2 CD (gt)
AB= CD (vì ABCD là hình chữ nhật)
Suy ra: AP = QD
Hay tứ giác APQD là hình bình hành.
Lại có: A = (vì tứ giác ABCD là hình chữ nhật)
Suy ra tứ giác APQD là hình chữ nhật.
Mà AD = AP = 1/2 AB
Vậy tứ giác APQD là hình vuông.
⇒ AQ ⊥ PD (t/chất hình vuông) ⇒ (PHQ) = (1)
HP = HQ (t/chất hình vuông)
* Xét tứ giác PBCQ, ta có: AB // CD hay BP //CQ
PB = 1/2 AB (gt)
CQ = 1/2 CD (gt)
AB = CD do ABCD là hình chữ nhật
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Lại có: B = (vì ABCD là hình chữ nhật) suy ra tứ giác PBCQ là hình chữ nhật
PB = BC ( vì cùng bằng AD = 1/2 AB)
Vậy tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (t/chất hình vuông) ⇒ (PKQ) = (2)
PD là tia phân giác (APQ) ( t/chất hình vuông)
PC là tia phân giác (QPB) (t/chất hình vuông)
Suy ra: PD ⊥ PC (t/chất tia phân giác của hai góc kề bù) ⇒ (HPK) = (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Copyright © 2021 HOCTAP247