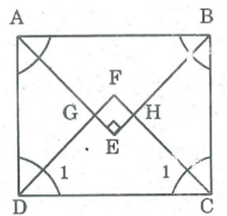
Cho hình chữ nhật có hai cạnh kề không bằng nhau. Chứng minh rằng các

* Hướng dẫn giải

Gọi giao điểm các đường phân giác của các góc: A, B, C, D theo thứ tự cắt nhau tại E, H, F, G.

* Trong $∆$ADG , ta có:

$\angle$(GAD) = ${45}^0$; $\angle$(GDA) = ${45}^0$ (gt)

Suy ra: $\angle$(AGD) = ${180}^0$ - $\angle$(GAD) - $\angle$(GDA) = ${90}^0$

⇒ $∆$GAD vuông cân tại G.

⇒ GD = GA

Trong $∆$BHC, ta có:

$\angle$(HBC) = ${45}^0$; $\angle$(HCB) = ${45}^0$ (gt)

Suy ra: $\angle$(BHC) = ${180}^0$ - $\angle$(HBC) - $\angle$(HCB) = ${90}^0$

⇒ $∆$HBC vuông cân tại H.

⇒ HB = HC

* Trong ΔFDC, ta có: $\angle$$D_1$ = ${45}^0$; $\angle$$C_1$= ${45}^0$ (gt)

Suy ra: $\angle$F = ${180}^0$ - D1 - C1 = ${90}^0$

⇒ $∆$FDC vuông cân tại F ⇒ FD = FC

Nên tứ giác EFGH là hình chữ nhật (vì có 3 góc vuông).

Xét $∆$GAD và $∆$HBC,ta có: $\angle$(GAD) = $\angle$(HBC) = ${45}^0$

AD = BC (tính chất hình chữ nhật)

$\angle$(GDA) = $\angle$(HCB) = ${45}^0$

Suy ra: $∆$GAD = $∆$HBC ( g.c.g)

Do đó, GD = HC .

Lại có: FD = FC (chứng minh trên)

Suy ra: FG = FH

Vậy hình chữ nhật EFGH có hai cạnh kề bằng nhau nên nó là hình vuông.