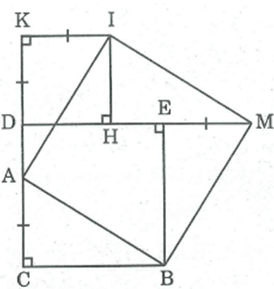
Cho hình vuông DEBC. Trên cạnh DC lấy điểm A, trên tia đối của tia

* Hướng dẫn giải

* Xét $∆$CAB và $∆$EMB, ta có:

CA = EM (gt)

$\angle$(ACB) = $\angle$(MEB) = ${90}^0$

CB = EB (tính chất hình vuông)

Suy ra: $∆$CAB = $∆$EMB (c.g.c)

⇒ AB = MB (1)

Ta có: AK = DK+ DA

CD = CA + AD

Mà CA = DK nên AK = CD

* Xét $∆$CAB và $∆$KIA, ta có:

CA = KI (vì cùng bằng DK)

$\angle$C = $\angle$K = ${90}^0$

CB = AK (vì cùng bằng CD)

Suy ra: $∆$CAB = $∆$KIA (c.g.c)

⇒ AB = AI (2)

Ta có: DH = DK (vì KDHI là hình vuông)

Và EM = DK (gt)

Suy ra: DH = EM

⇒ DH + HE = HE + EM

Hay DE = HM

* Xét $∆$HIM và $∆$EMB, ta có: HI = EM (vì cũng bằng DK)

$\angle$H = $\angle$E = ${90}^0$

HM = EB (vì cùng bằng DE)

Suy ra: $∆$HIM = $∆$EMB (c.g.c)

⇒ IM = MB (3)

Từ (1) , (2) và (3) suy ra: AB = BM = AI = IM

Tứ giác ABMI là hình thoi.

Mặt khác, ta có $∆$ACB = $∆$MEB (chứng minh trên)

⇒ $\angle$(CBA) = $\angle$(EBM)

Mà $\angle$(CBA) + $\angle$(ABE) = $\angle$(CBE) = ${90}^0$

Suy ra: $\angle$(EBM) + $\angle$(ABE) = ${90}^0$ hay $\angle$(ABM) = ${90}^0$

Vậy tứ giác ABMI là hình vuông.