Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia...
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE
Câu hỏi :
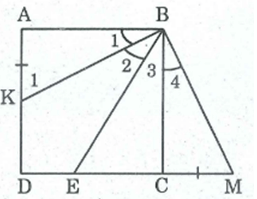
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng AK+CE = BE.
* Đáp án
* Hướng dẫn giải
Trên tia đối của tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (1)
Xét ABK và CBM, ta có:
AB = CB (gt)
A = C =
AK = CM (theo cách vẽ)
Suy ra: ABK = CBM (c.g.c)
⇒ = (2)
Lại có: = ( do BK là tia phân giác của ABE)
Suy ra: = =
Mà (KBC) = - (3)
Tam giác CBM vuông tại C nên: M = - (4)
Từ (2), (3) và (4) suy ra: (KBC) = M (5)
Hay + = M
⇒ + = M( vì = )
Hay: (EBM) = M
⇒ EBM cân tại E ⇒ EM = BE. (6)
Từ (1) và (6) suy ra: AK + CE = BE.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247