Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là một hình thoi
Câu hỏi :
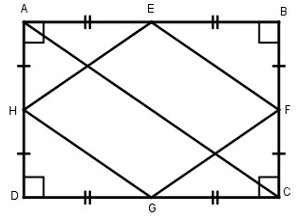
Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là một hình thoi.
* Đáp án
* Hướng dẫn giải
Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA của hình chữ nhật ABCD.
Kẻ đường chéo AC, BD
* Trong ABC, ta có:
E là trung điểm của AB
F là trung điểm của BC
Nên EF là đường trung bình của ABC.
⇒ EF // AC và EF = 1/2 AC (t/chất đường trung bình của tam giác) (1)
Trong ADC, ta có: H là trung điểm của AD
G là trung điểm của DC
Nên HG là đường trung bình của tam giác ADC.
⇒ HG // AC và HG = 1/2 AC (t/chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Xét AEH và DGH, ta có: AH = HD (gt)
EAH và GDH =
AE = DG (vì AB = CD)
Suy ra: AEH = DGH (c.g.c) ⇒ HE = HG
Vậy hình bình hành EFGH là hình thoi (hình bình hành có 2 cạnh kề bằng nhau).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Copyright © 2021 HOCTAP247