Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một
Câu hỏi :
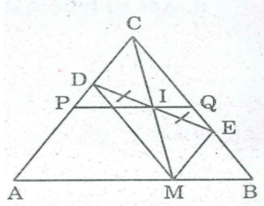
Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào?
* Đáp án
* Hướng dẫn giải
Gọi C là giao điểm của AD và BE.
Tam giác ABC có:
A = (vì ΔADM đều)
B = ( vì ΔBEM đều)
Nên C = - A - B =
Suy ra: ABC đều hay AB = AC = BC
Suy ra điểm C cố định.
Lại có: A = (EMB ) =
ME // AC ( vì có cặp góc đồng vị bằng nhau)
Hay ME // CD.
Do DMA = BEM = ( hai tam giác AMD và BME là tam giác đều )
Suy ra: MD // BC ( vì có cặp góc so le trong bằng nhau ).
hay MD // EC
suy ra tứ giác CDME là hình bình hành.
I là trung điểm của DE nên I là trung điểm của CM
Kẻ CH ⊥ AB,IK ⊥ AB⇒IK // CH
Trong CHM,ta có:CI = IM và IK // CH
Suy ra IK là đường trung bình của ΔCHM⇒IK = 1/2 CH
Vì C cố định nên CH không đổi ⇒ IK = 1/2 CH không đổi nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng 1/2 CH
Khi M trùng với A thì I trùng với trung điểm P của AC.
Khi M trùng với B thì I trùng với trung điểm Q của BC.
Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ ( P là trung điểm AC, Q là trung điểm BC).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Copyright © 2021 HOCTAP247