Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
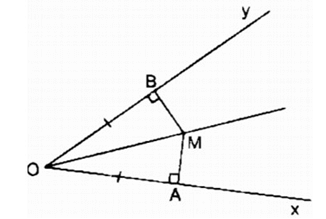
Cho góc xOy cố định khác góc bẹt. Các điểm...
Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự
Câu hỏi :
Cho góc xOy cố định khác góc bẹt. Các điểm A và B theo thứ tự chuyển động trên các tia Ox và Oy sao cho OA = OB. Đường vuông góc với OA tại A và đường vuông góc với OB tại B cắt nhau ở M. Điểm M chuyển động trên đường nào ?
* Đáp án
* Hướng dẫn giải
Xét hai tam giác vuông MOA và MOB: (MAO) = (MBO) =
OA = OB (gt)
OM cạnh huyền chung
Do đó: MAO = MBO (cạnh huyền, cạnh góc vuông)
⇒(AOM) = (BOM)
A và B thay đổi, OA và OB luôn bằng nhau nên MAO và MBO luôn luôn bằng nhau do đó (AOM) = (BOM)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247