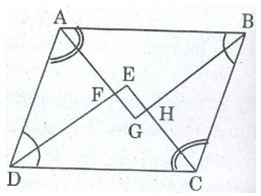
Chứng minh rằng các tia phân giác các góc của hình bỉnh hành cắt nhau

* Hướng dẫn giải

Gọi G, H, E, F lần lượt là giao điểm của các đường phân giác của $\angle$A và $\angle$B; $\angle$B và $\angle$C; $\angle$C và $\angle$D; $\angle$D và $\angle$A

Ta có: $\angle$(ADF) = 1/2 $\angle$(ADC) (gt)

$\angle$(DAF) = 1/2 $\angle$(DAB) (gt)

$\angle$(ADC) + $\angle$(DAB) = ${180}^0$ (hai góc trong cùng phía)

Suy ra: $\angle$(ADF) + $\angle$(DAF) = 1/2 ($\angle$(ADC) + $\angle$(DAB) ) = 1/2 .${180}^0$ = ${90}^0$

Trong $∆$AFD, ta có:

$\angle$(AFD) = ${180}^0$ – ($\angle$(ADF) + $\angle$(DAF)) = ${180}^0$ – ${90}^0$ = ${90}^0$

$\angle$(EFG) = $\angle$(AFD) (đối đỉnh)

⇒ $\angle$(EFG) = ${90}^0$

$\angle$(GAB) = 1/2 $\angle$(DAB) (gt)

$\angle$(GBA) = 1/2 $\angle$(CBA) (gt)

$\angle$(DAB) + $\angle$(CBA) = ${180}^0$ (hai góc trong cùng phía)

⇒ $\angle$(GAB) + $\angle$(GBA) = 1/2 ($\angle$(DAB) + $\angle$(CBA) ) = 1/2 .${180}^0$ = ${90}^0$

Trong ΔAGB ta có: $\angle$(AGB) = ${180}^0$ – ($\angle$(GAB) + $\angle$(GBA) ) = ${180}^0$ - ${90}^0$ = ${90}^0$

Hay $\angle$G = ${90}^0$

$\angle$(EDC) = 1/2 $\angle$(ADC) (gt)

$\angle$(ECD) = 1/2 $\angle$(BCD) (gt)

$\angle$(ADC) + $\angle$(BCD) = ${180}^0$ (hai góc trong cùng phía)

⇒ $\angle$(EDC) + $\angle$(ECD) = 1/2 (∠$\angle$ADC) + $\angle$(BCD) ) = 1/2 .${180}^0$ = ${90}^0$

Trong ΔEDC ta có: $\angle$(DEC) = ${180}^0$ – ($\angle$(EDC) + $\angle$(ECD) ) = ${180}^0$ - ${90}^0$ = ${90}^0$

Hay $\angle$E = ${90}^0$

Vậy tứ giác EFGH là hình chữ nhật (vì có ba góc vuông).