Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Chứng minh rằng ba điểm C, B, D ở hình...
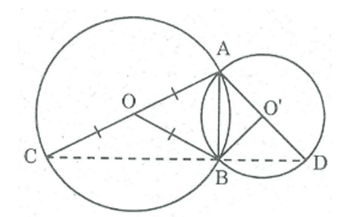
Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng
Câu hỏi :
Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng.
* Đáp án
* Hướng dẫn giải
Nối AB, BO, BC, BO', BD.
* Trong ABC, ta có: OA = OC = R (bán kính đường tròn (O))
Nên BO là đường trung tuyến của ABC.
Mà BO = R (bán kính (O)) ⇒ BO = OA= OC = 1/2 AC
Suy ra tam giác ABC vuông tại B ⇒ (ABC) =
* Trong ABD , ta có: AO' = O'D = R' (bán kính đường tròn (O'))
Nên BO' là đường trung tuyến của tam giác ABD.
Mà BO' = R' (bán kính (O')) ⇒ BO' = AO' = O'D = 1/2 AD
Suy ra tam giác ABD vuông tại B ⇒ (ABD) =
Ta có: (ABC) + (ABD) = (CBD) = + =
Vậy C, B, D thẳng hàng.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247