Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho tam giác ABC, D là trung điểm của AB,...
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC
Câu hỏi :
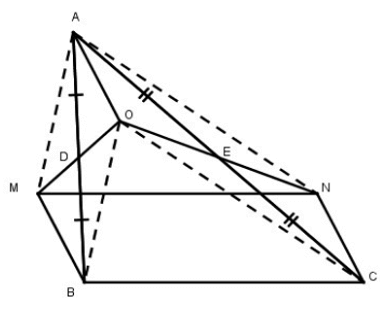
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kỳ nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D. Vẽ điểm N đối xứng với O qua E. Chứng minh rằng MNCB là hình bình hành.
* Đáp án
* Hướng dẫn giải
* Xét tứ giác AOBM, ta có:
DA = DB (gt)
DO = DM (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ BM // AO và BM = AO (1)
* Xét tứ giác AOCN, ta có: EA = EC (gt)
EO = EN (định nghĩa đối xứng tâm)
Suy ra: Tứ giác AOCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ CN // AO và CN = AO (2)
Từ (1) và (2) suy ra:BM // CN và BM = CN.
Vậy tứ giác BMNC là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247