Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho tam giác ABC, các đường trung tuyến AD, BE,...
Cho tam giác ABC, các đường trung tuyến AD, BE, CF cắt nhau tại G
Câu hỏi :
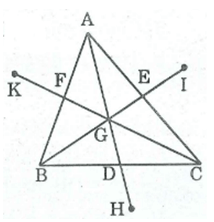
Cho tam giác ABC, các đường trung tuyến AD, BE, CF cắt nhau tại G. Gọi H là điểm đối xứng với G qua D, I là điểm đối xứng với G qua E, K là điểm đối xứng với G qua F. Tìm các điểm đối xứng với A, với B, với C qua G.
* Đáp án
* Hướng dẫn giải
*) Tam giác ABC có ba đường trung tuyến AD, BE, CF cắt nhau tại G nên G là trọng tâm tam giác ABC.
* Ta có: GD = DH (tính chất đối xứng tâm)
⇒ GH = 2GD (l)
GA = 2GD (tính chất đường trung tuyến của tam giác) (2)
Từ (1) và (2) suy ra: GA = GH
Suy ra điểm đối xứng với điểm A qua G là H.
* Ta có: GE = EI (tính chất đối xứng tâm)
⇒ GI = 2GE (3)
Lại có, GB = 2GE (tính chất đường trung tuyến của tam giác) (4)
Từ (3) và (4) suy ra: GB = GI
Suy ra điểm đối xứng với điểm B qua G là I.
+) Ta có: GF = FK (tính chất đối xứng tâm)
⇒ GK = 2GF (5)
GC = 2GF (tính chất đường trung tuyến của tam giác) (6)
Từ (5) và (6) suy ra: GC = GK
Suy ra điểm đối xứng với điểm C qua G là điểm K
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247