Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
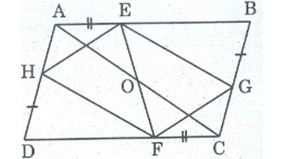
Hình dưới cho ABCD là hình bình hành. Chứng minh...
Hình dưới cho ABCD là hình bình hành. Chứng minh rằng: EGFH là hình bình
Câu hỏi :
Hình dưới cho ABCD là hình bình hành. Chứng minh rằng: EGFH là hình bình hành.
* Đáp án
* Hướng dẫn giải
+) Ta có: AH + HD = AD
CG + GB = CB
Mà AD = CB ( vì ABCD là hình bình hành).
DH = GB ( giả thiết)
Suy ra: AH = CG.
Xét AEH và CFG:
AE = CF (gt)
A = C (tính chất hình bình hành)
AH = CG ( chứng minh trên).
Do đó: AEH = CFG (c.g.c)
⇒ EH = FG
Xét BEG và DFH, ta có:
BG = DH (gt)
B = D (tính chất hình bình hành)
BE = DF (vì AB = CD và AE = CF nên AB – AE = CD – CF hay BE = DF )
Do đó: BEG = DFH (c.g.c) ⇒ EG = FH
Suy ra: Tứ giác EGFH là hình bình hành (vì có các cặp cạnh đối bằng nhau)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247