Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho hình bình hành ABCD có A = anpha >...
Cho hình bình hành ABCD có A = anpha > 90 độ. Ở phía ngoài hình bình hành
Câu hỏi :
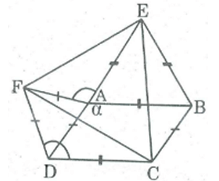
Cho hình bình hành ABCD có A = > . Ở phía ngoài hình bình hành vẽ các tam giác đều ADF, ABE. Chứng minh rằng tam giác CEF là tam giác đều.
* Đáp án
* Hướng dẫn giải
Ta có:
(BAD) + ∠(ADC) = (hai góc trong cùng phía bù nhau)
⇒ (ADC) = - (BAD) = –
(CDF) = (ADC) + (ADF) = -
Suy ra: (CDF) = (EAF)
Xét AEF và DCF: AF = DF ( vì ADF đều)
AE = DC (vì cùng bằng AB)
(CDF) = (EAF) (chứng minh trên)
Do đó: AEF = DCF (c.g.c) ⇒ EF = CF (1)
(CBE) = (ABC) +
Xét ΔBCE và ΔDFC: BE = CD ( vì cùng bằng AB)
(CBE) = (CDF) =
BC = DF (vì cùng bằng AD)
Do đó BCE = DFC (c.g.c) ⇒ CE = CF (2)
Từ (1) và (2) suy ra: EF = CF = CE
Vậy ECF đều.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247