Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho tam giác ABC, các đường trung tuyến BD và...
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G
Câu hỏi :
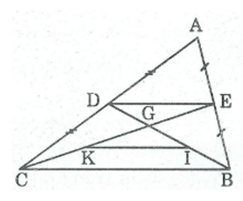
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE//IK, DE= IK.
* Đáp án
* Hướng dẫn giải
* Trong ABC, ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của ABC
⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)
* Trong GBC, ta có:
I là trung điểm của BG (gt)
K là trúng điểm của CG (gt)
Nên IK là đường trung bình của GBC
⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)
Từ (l) và (2) suy ra: IK // DE, IK = DE.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247