Chứng minh rằng trong hình thang mà hai đáy không bằng nhau, đoạn thẳng

* Hướng dẫn giải

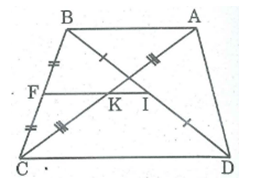
Giả sử hình thang ABCD có AB // CD, AB < CD

Gọi I, K lần lượt là trung điểm hai đường chéo BD, AC; F là trung điểm của BC.

* Trong $∆$ACB, ta có:

K là trung điểm của cạnh AC

F là trung điểm của cạnh BC

Nên KF là đường trung bình của $∆$ACB

⇒ KF // AB và KF = 1/2 AB

(tính chất đường trung bình của tam giác)

Trong $∆$BDC, ta có: I là trung điểm của cạnh BD

F là trung điểm của cạnh BC

Nên IF là đường trung bình của $∆$BDC

⇒ IF // CD và IF = 1/2 CD (tính chất đường trung bình của tam giác)

FK // AB mà AB // CD nên FK // CD

FI // CD (chứng minh trên)

Suy ra hai đường thẳng FI và FK trùng nhau.

⇒ I, K, F thẳng hàng, AB < CD ⇒ FK < FI nên K nằm giữa I và F

IF = IK + KF

⇒ IK = IF – KF = 1/2 CD - 1/2 AB = (CD - AB)/2