Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Hình thang ABCD có AB // CD; AB = a,...
Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các
Câu hỏi :
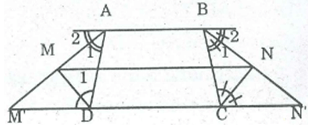
Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các đường phân giác của góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Chứng minh rằng MN // CD
* Đáp án
* Hướng dẫn giải
Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: (M') = (sole trong)
= (gt)
⇒ (M') = nên ADM' cân tại D
* DM là phân giác của (ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
(N') = nên BCN' cân tại C.
* CN là phân giác của (BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN // M'N' (tính chất đường trung hình hình thang)
Hay MN//CD
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247