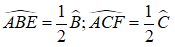Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Cho tam giác ABC cân tại A, các đường phân...
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng
Câu hỏi :
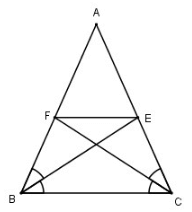
Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
* Đáp án
* Hướng dẫn giải
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
Mà tam giác ABC cân tại A nên B = C
Suy ra: ABE = ACF
Xét hai tam giác AEB và AFC
Có AB = AC (ABC cân tại A)
ABE = ACF (chứng minh trên)
A là góc chung
⇒ AEB = AFC (g.c.g) ⇒ AE = AF ⇒ AEF cân tại A
⇒ AFE = (− A) / 2 và trong tam giác ABC: B = (− ∠A) / 2
⇒AFE = B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Vì FE//BC nên ta có: FEB = EBC (so le trong)
Lại có: FBE = EBC ( vì BE là tia phân giác của góc B)
⇒FBE = FEB
⇒ FBE cân ở F ⇒ FB = FE
⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247