Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
Hai đoạn thẳng AB và CD cắt nhau tại 0....
Hai đoạn thẳng AB và CD cắt nhau tại 0. Biết rằng OA = OC, OB = OD
Câu hỏi :
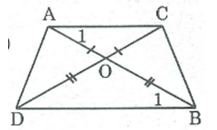
Hai đoạn thẳng AB và CD cắt nhau tại 0. Biết rằng OA = OC, OB = OD. Tứ giác ABCD là hình gì ? Vì sao
* Đáp án
* Hướng dẫn giải
Ta có: OA = OC (gt)
⇒ OAC cân tại O
⇒= ( - (AOC) ) / 2 (tính chất tam giác cân) (1)
OB = OD (gt)
⇒ OBD cân tại O
⇒ = ( - (BOD) )/2 (tính chất tam giác cân) (2)
(AOC) = (BOD) (đối đỉnh) (3)
Từ (1), (2), (3) suy ra: =
⇒ AC // BD (vì có cặp góc ở vị tri so le trong bằng nhau)
Suy ra: Tứ giác ACBD là hình thang
Ta có: AB = OA + OB
CD = OC + OD
Mà OA = OC, OB = OD
Suy ra: AB = CD
Vậy hình thang ABCD là hình thang cân.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247