Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải Sách Bài Tập Toán 8 Tập 1 !!
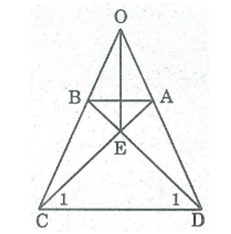
Hình thang cân ABCD có 0 là giao điểm của...
Hình thang cân ABCD có 0 là giao điểm của hai đường thắng chứa
Câu hỏi :
Hình thang cân ABCD có 0 là giao điểm của hai đường thắng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.
* Đáp án
* Hướng dẫn giải
Ta có: (ADC) = (BCD) (gt)
⇒ (ODC) = (OCD)
⇒OCD cân tại O
⇒ OC = OD
OB + BC = OA + AD
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ADC và BCD:
AD = BC (tính chất hình thang cân )
AC = BD (tính chất hình thang cân)
CD chung
Do đó ADC và BCD (c.c.c)
⇒ =
⇒EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực CD
OC = OD nên O thuộc đường trung trực CD
E O. Vậy OE là đường trung trực của CD.
Ta có: BD= AC (tính chất hình thang cân)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB
E O. Vậy OE là đường trung trực của AB.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 8 Tập 1 !!
Số câu hỏi: 794
Copyright © 2021 HOCTAP247