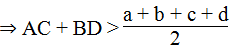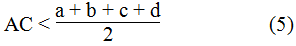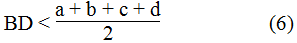Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu

* Hướng dẫn giải

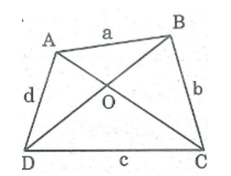
Đặt độ dài a = AB, b = BC, c = CD, d = AD

Gọi O là giao điểm 2 đường chéo AC và BD.

* Trong $∆$OAB, ta có:

OA + OB > a (bất đẳng thức tam giác) (1)

* Trong $∆$OCD, ta có:

OC + OD > c (bất đẳng thức tam giác) (2)

Từ (1) và (2) suy ra:

OA + OB + OC + OD > a + c hay AC + BD > a + c (*)

* Trong $∆$ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)

* Trong $∆$OBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)

Từ (3) và (4) suy ra:

OA + OB + OC + OD > b + d hay AC + BD > b + d (**)

Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d

* Trong $∆$ABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)

* Trong $∆$ADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)

Suy ra: 2AC < a + b + c + d

* Trong $∆$ABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)

* Trong $∆$BCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)

Suy ra: 2BD < a + b + c + d

Từ (5) và (6) suy ra: AC + BD < a + b + c + d