Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Tổng hợp Lý thuyết & Trắc nghiệm Chương 1 Hình học 8 !!
Tính chiều cao BH của hình thang cân ABCD, biết...
Tính chiều cao BH của hình thang cân ABCD, biết AC vuông góc với BD
Câu hỏi :
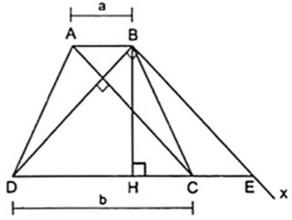
Tính chiều cao BH của hình thang cân ABCD, biết AC ⊥ BD và hai cạnh đáy AB = a, CD = b. Từ đó suy ra cách vẽ hình.
* Đáp án
* Hướng dẫn giải
Kẻ Bx ⊥ BD cắt DC tại E, do cùng với vuông góc với BD.
Hình thang ABEC có hai cạnh bên song song, nên AC = BE ( 1 ) và hai đáy AB = CE = a.
Suy ra DE = DC + CE = a + b
Lại có: AC = BD (vì là đường chéo của hình thang cân) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra BD = BE nên tam giác BDE vuồn cân tại B.
Do BH vừa là đường cao vừa là đường trung tuyến của tam giác BDE, nên
Lúc đó tam giác BDH vuông cân tại H.
Vậy BH = (a + b)/2.
Cách vẽ hình:
+ Bước 1: Vẽ Δ BDE vuông cân tại B có đường cao BH và DE = a + b.
+ Bước 2: Kẻ Bx//DE. Lấy C ∈ HE sao cho CE = b.
+ Bước 3: Kẻ Cy//DE cắt Bx tại A. Ta được hình thang thỏa mãn yêu cầu bài cho.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp Lý thuyết & Trắc nghiệm Chương 1 Hình học 8 !!
Số câu hỏi: 70
Copyright © 2021 HOCTAP247