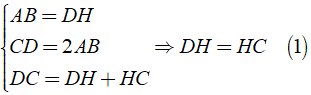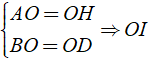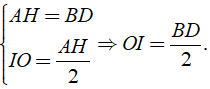Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Tổng hợp Lý thuyết & Trắc nghiệm Chương 1 Hình học 8 !!
Cho hình thang vuông ABCD có góc A = góc...
Cho hình thang vuông ABCD có góc A = góc D = 90 độ và CD = 2AB
Câu hỏi :
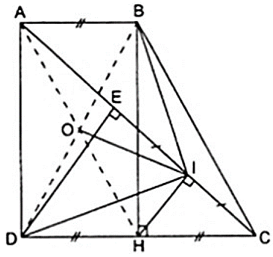
Cho hình thang vuông ABCD có và CD = 2AB. Kẻ DE ⊥ AC, gọi I là trung điểm của EC. Chứng minh rằng .
* Đáp án
* Hướng dẫn giải
Vẽ BH ⊥ DC thì tứ giác ABHD có ba góc vuông là nên nó là hình chữ nhật.
Áp dụng tính chất về cạnh và giả thiết về hình chữ nhật ABHD ta được:
Lại có IE = IC ( 2 )
Từ ( 1 ), ( 2 ) suy ra HI là đường trung bình của tam giác DCE.
Áp dụng định lý về được trung bình trong tam giác DCE ta được HI//DE do DE ⊥ AC theo giả thiết nên HI ⊥ AC hay tam giác AIH vuông tại I.
+ Trong hình chữ nhật ABHD có
là đường trung tuyến của hai tam giác vuông AIH và BID.
Mặt khác ta lại có:
Điều đó chứng tỏ trong tam giác BID có IO là đường trung tuyến ứng với cạnh huyền và bằng nửa cạnh ấy nên nó là tam giác vuông tại I.
Vậy
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Tổng hợp Lý thuyết & Trắc nghiệm Chương 1 Hình học 8 !!
Số câu hỏi: 70
Copyright © 2021 HOCTAP247