Cho hình bình hành ABCD có góc A là góc tù. Kẻ AH và CK vuông góc với

* Hướng dẫn giải

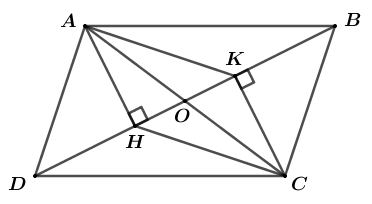
a) Chứng minh rằng: Tứ giác AHCK là hình bình hành.

+) ABCD là hình bình hành

$\Rightarrow \left\{\begin{array}{l}\mathrm{AB}=\mathrm{DC};\mathrm{AD}=\mathrm{BC}\\ \mathrm{AB}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{DC};\mathrm{AD}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{BC}\end{array}\right.$ (tính chất của hình bình hành)

+) $\left.\begin{array}{l}\mathrm{CK}\perp \mathrm{BD}\left(\mathrm{gt}\right)\\ \mathrm{AH}\perp \mathrm{BD}\left(\mathrm{gt}\right)\end{array}\right\}\Rightarrow \mathrm{CK}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{AH}$ (quan hệ từ vuông góc đến song song)   (1)

+) Vì AD // BC nên $\widehat{\mathrm{ADB}}=\widehat{\mathrm{DBC}}$ (hai góc so le trong)

Xét $\mathrm{\Delta ADH}$ và $\mathrm{\Delta CBK}$ có:

$\widehat{\mathrm{AHD}}=\widehat{\mathrm{BKC}}={90}^{\circ }$

AD = BC (cmt)

$\widehat{\mathrm{ADH}}=\widehat{\mathrm{BKC}}$ (cmt)

$\Rightarrow \mathrm{\Delta ADH}=\mathrm{\Delta CBK}$ (cạnh huyền – góc nhọn)

=> AH = CK (hai cạnh tương ứng)   (2)

Từ (1) và (2) suy ra AHCK là hình bình hành (dấu hiệu nhận biết).

b) Gọi O là trung điểm của HK. Chứng minh ba điểm A, O, C thẳng hàng.

Theo tính chất, AHCK là hình bình hành nên hai đường HK và AC cắt nhau tại trung điểm của mỗi đường.

Theo đề bài, O là trung điểm của HK nên O là trung điểm của AC.

Do đó, ba điểm A, O, C thẳng hàng.

c) Tính diện tích hình bình hành AHCK. Biết AH = 4cm, HK = 2cm.

Ta có:

${\mathrm{S}}_{\mathrm{AHK}}=\frac{1}{2}.\mathrm{AH}.\mathrm{HK}$

${\mathrm{S}}_{\mathrm{CHK}}=\frac{1}{2}.\mathrm{CK}.\mathrm{HK}$

Mà AH = CK nên ${\mathrm{S}}_{\mathrm{AHK}}={\mathrm{S}}_{\mathrm{CHK}}$.

$\Rightarrow {\mathrm{S}}_{\mathrm{AKCH}}={\mathrm{S}}_{\mathrm{AHK}}+{\mathrm{S}}_{\mathrm{CHK}}=2{\mathrm{S}}_{\mathrm{AHK}}=\mathrm{AH}.\mathrm{HK}$$=4.2=8\left({\mathrm{cm}}^2\right)$

Vậy ${\mathrm{S}}_{\mathrm{AKCH}}=8{\mathrm{cm}}^2$