Cho tam giác ABC vuông tại A, AB = 4cm, AC = 8cm. Gọi E là trung điểm

* Hướng dẫn giải

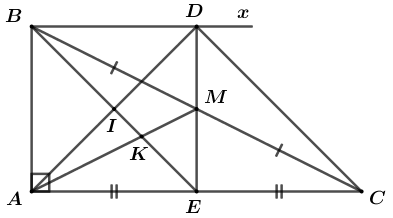
a) Tính EM.

Xét tam giác ABC ta có:

M là trung điểm của BC

E là trung điểm của AC

=> EM là đường trung bình của tam giác ABC

$\Rightarrow \mathrm{EM}=\frac{1}{2}\mathrm{AB}=6\mathrm{cm}$

b) Vẽ tia Bx song song với AC sao cho Bx cắt EM tại D. Chứng minh rằng tứ giác ABDE là hình vuông.

Vì EM là đường trung bình của $\mathrm{\Delta ABC}$ nên EM // AB.

=> ED // AB

Ta lại có: $\left.\begin{array}{l}\mathrm{D}\in \mathrm{Bx}\\ \mathrm{Bx}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{AE}\end{array}\right\}\Rightarrow \mathrm{BD}\text{\hspace{0.17em}//\hspace{0.17em}}\mathrm{AE}$

Xét tứ giác ABDE ta có:

ED // AB

BD // AE

=> Tứ giác ABDE là hình bình hành (dấu hiệu nhận biết)

$$\begin{gathered} \left.\begin{array}{l}\left.\begin{array}{l}\mathrm{AB}=4\mathrm{cm}\\ \mathrm{AC}=8\mathrm{cm}\end{array}\right\}\Rightarrow \mathrm{AB}=\frac{1}{2}\mathrm{AC}\\ \mathrm{AE}=\mathrm{EC}=\frac{1}{2}\mathrm{AC}\end{array}\right\} \\ \Rightarrow \mathrm{AE}=\mathrm{AB} \end{gathered}$$

=> Hình bình hành ABDE là hình thoi (dấu hiệu nhận biết)

Mà $\widehat{\mathrm{BAE}}={90}^{\circ }$ nên hình thoi ABDE là hình vuông (dấu hiệu nhận biết)

c) Gọi I là giao điểm của BE và AD. Gọi K là giao điểm của BE với AM. Chứng minh rằng: Tứ giác BDCE là hình bình hành và DC = 6IK.

Vì ABDE là hình vuông nên:

+ BD // AE => BD // EC

+ $\left.\begin{array}{l}\mathrm{BD}=\mathrm{AE}\\ \mathrm{AE}=\mathrm{EC}\end{array}\right\}\Rightarrow \mathrm{BD}=\mathrm{EC}$

Xét tứ giác BDCE ta có:

BD // EC

BD = EC

Suy ra, tứ giác BDEC là hình bình hành (dấu hiệu nhận biết).

=> BE = CD (tính chất)

Theo đề bài, ta có: ABDE là hình vuông có I là giao điểm hai đường chéo

$\Rightarrow \mathrm{IA}=\mathrm{IB}=\mathrm{ID}=\mathrm{IE}=\frac{1}{2}\mathrm{BE}$

Xét $\mathrm{\Delta ADE}$ có:

EI là đường trung tuyến ứng với AD

AM là đường trung tuyến ứng với DE

Mà K là giao điểm của AM và EI. Suy ra. K là trọng tâm $\mathrm{\Delta ADE}$.

 $\text{⇒IK=}\frac{1}{3}\mathrm{IE}=\frac{1}{6}\mathrm{BE}=\frac{1}{6}\mathrm{DC}$

=> DC = 6IK (đpcm)