Đề kiểm tra 15 phút - Đề số 17 - Bài 2, 3, 4, 5 - Chương 2 - Hình học 7
Tóm tắt bài
Đề bài
Cho tam giác ABC, đường trung trực d1 của đoạn thẳng BC và đường trung trực d2 của đoạn thẳng AC cắt nhau tại O.
a) Chứng minh \(OA = OB = OC.\)
b) Gọi M là trung điểm của đoạn AB. Chứng minh OM là đường trung trực của đoạn AB.
Hướng dẫn giải
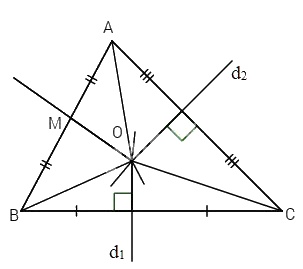
a) d1 là trung trực của đoạn thẳng BC\( \Rightarrow OB = OC\).
Tương tự d2 là trung trực của AC \( \Rightarrow OC = OA.\)
Do đó \(OA = OB = OC.\)
b) Xét \(\Delta OMA \) và \( \Delta OMB\) có
+) OM chung
+) OA = OB (chứng minh trên)
+) MA = MB (giả thiết).
Vậy \(\Delta OMA = \Delta OMB\) (c.c.c)
\( \Rightarrow \widehat {OAM} = \widehat {OMB}\) (góc tương ứng) mà \(\widehat {OAM} + \widehat {OMB} = {180^o}\) (cặp góc kề bù)
\( \Rightarrow \widehat {OAM} = \widehat {OMB} = {90^o}\).
Chứng tỏ \(OM \bot AB.\)
Mà M là trung điểm của AB. Do đó OM là đường trung trực của AB.
Copyright © 2021 HOCTAP247
