Giải bài 35 trang 123 - Sách giáo khoa Toán 7 tập 1

Đề bài

Cho góc xOy khác gọc bẹt Ot là tia phân giác của góc đó. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với tia Ot, nó cắt Ox và Oy theo thứ tự ở A và B.

a) Chứng minh rằng OA = OB

b) Lấy điểm C thuộc tia Ot. Chứng minh rằng

Hướng dẫn giải

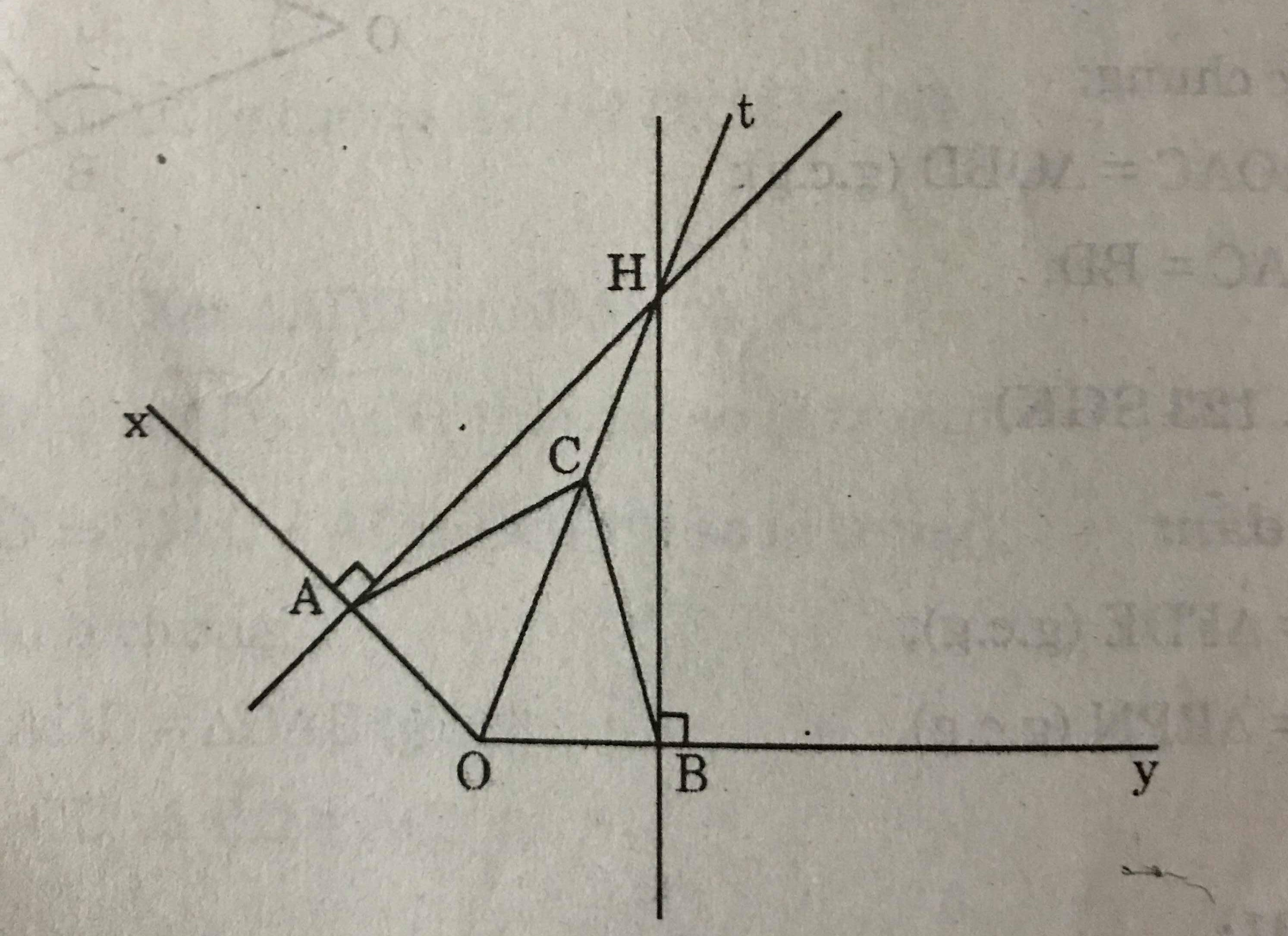
a) Chứng minh OA = OB

Xét hai tam giác vuông ΔOAH = ΔOBH có :

\(\widehat{A}\) = \(\widehat{B}\) ( = \(90^0\) )

\(\widehat{HOA}\) = \(\widehat{HOB}\) ( tính chất tia phân giác của góc )

OH : cạnh chung

Do đó : ΔOAH = ΔOBH (c.g.c)

Suy ra : OA = OB (hai cạnh tương ứng)

b) Xét ΔAOC và ΔBOC có :

OA = OB (câu a)

\(\widehat{AOC}\) = \(\widehat{BOC}\) ( tính chất tia phân giác của góc )

OC :  cạnh chung

Do đó : ΔAOC và ΔBOC (c.g.c)

Suy ra : CA = CB và \(\widehat{OAC}\) = \(\widehat{OBC}\) (hai góc và hai cạnh tương ứng)