Đề kiểm tra 15 phút - Đề số 4 - Bài 2,3,4,5 - Chương 2 - Hình học 7
Tóm tắt bài
Đề bài
Cho tam giác ABC, M là trung điểm của BC. Trên nửa mặt phẳng bờ là đường thẳng BC chứa điểm A vẽ tia Cx song song với AB. Trên tia Cx lấy D sao cho \( \Rightarrow \widehat {AMC} + \widehat {CMD} = {180^o}\), \(CD = AB\). Chứng minh:
a)\(MA = MD.\)
b) Ba điểm A, M, D thẳng hàng.
Hướng dẫn giải
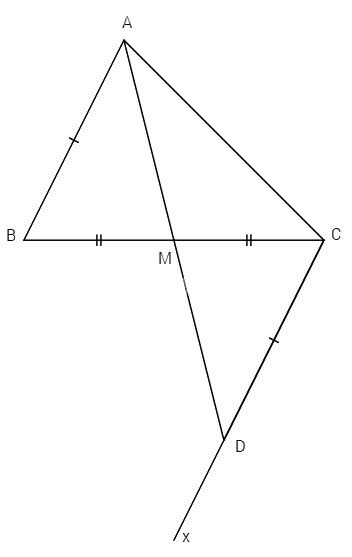
a) Ta có Cx // AB \( \Rightarrow \widehat {ABC} = \widehat {DCB}\) (cặp góc so le trong).
Xét \(\Delta ABM\) và \(\Delta DCM\) có:
+) MB = MC (giả thiết)
+) \(\widehat {ABC} = \widehat {DCB}\) (chứng minh trên)
+) AB = CD (giả thiết)
Do đó \(\Delta ABM=\Delta DCM\) (c.g.c)
\( \Rightarrow MA = MD\) (cạnh tương ứng)
b) Ta có \(\Delta ABM=\Delta DCM\) (chứng minh trên)
\( \Rightarrow \widehat {BMA} = \widehat {CMD}\) (góc tương ứng)
Mà \(\widehat {BMA} + \widehat {AMC} = {180^o}\) (cặp góc kề bù)
\( \Rightarrow \widehat {AMC} + \widehat {CMD} = {180^o}\)
Vậy ba điểm A, M, D thẳng hàng.
Copyright © 2021 HOCTAP247
