Bài 62 trang 83 SGK Toán 7 tập 2

Đề bài

Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.

Hướng dẫn giải

Ta chứng mình tam giác cân bằng cách chứng minh hai góc ở đáy bằng nhau.

Lời giải chi tiết

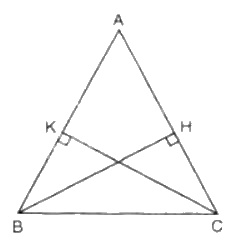
Vẽ BH ⊥ AC và CK ⊥ AB

Xét hai tam giác vuông KBC và HCB có:

BC (cạnh huyền chung)

BH = CK (gt)

Vậy ∆KBC = ∆HCB (cạnh huyền - cạnh góc vuông)

\( \Rightarrow \; \widehat{KBC}= \widehat{HCB}\)

Xét tam giác ABC ta có \(\widehat{KBC}= \widehat{HCB}\) hay \(\widehat{ABC}= \widehat{ACB}\)

 Vậy ∆ABC cân tại A (đpcm).

Chứng minh trên ta có:

    Nếu BH = CK thì ΔABC cân tại A \( \Rightarrow \) AB = AC (1)

    Nếu AI = BH thì ΔABC cân tại C  \( \Rightarrow \) CA = CB (2)

Từ (1) và (2) ta có: AB = BC = AC

Vậy ΔABC là tam giác đều (đpcm).