Đề kiểm tra 15 phút - Đề số 5 - Bài 9 - Chương 3 – Hình học 7
Tóm tắt bài
Đề bài
Cho tam giác ABC vuông tại A, đường cao AH, phân giác AD. Gọi I là giao điểm các đường phân giác của \(\Delta AHB\) và J là giao điểm các đường phân giác của \(\Delta AHC\) . Gọi E là giao điểm của các đường thẳng BI và AJ. Chứng minh rằng:
a) \(\Delta ABE\) là tam giác vuông;
b) \(IJ \bot A{\rm{D}}.\)
Hướng dẫn giải
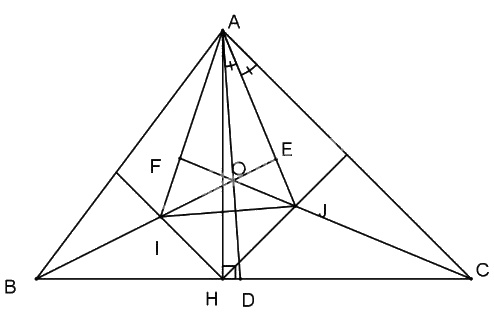
a) Ta có \(\widehat B = \widehat {HAC}\) (cùng phụ với \(\widehat C\))
\( \Rightarrow {{\widehat B} \over 2} = {{\widehat {HAC}} \over 2}\) hay \({\widehat B_1} = {\widehat A_2},\) mà \({\widehat A_2} + \widehat {BA{\rm{E}}} = {90^0}\) (vì \(\widehat {BAC} = {90^0}\))
\( \Rightarrow {\widehat B_1} + \widehat {BA{\rm{E}}} = {90^0}.\)
Trong \(\Delta A{\rm{E}}B \Rightarrow \widehat {BE{\rm{A}}} = {90^0}\) hay \(\Delta {\rm A}{\rm B}{\rm E}\) vuông tại E.
b) (Xem hình vẽ)
F là giao của CJ và AI
Chứng minh tương tự ta có \(CF \bot AI\) hay \(JF \bot AI\), lại có \(IE \bot {\rm A} J\) (cmt).
Gọi O là giao điểm của BI và CJ ta có O thuộc AD (giao điểm 3 đường phân giác của \(\Delta ABC\)) đồng thời O là trực tâm của \(\Delta AIJ\) \( \Rightarrow AO\) là đường cao thứ ba của \(\Delta AIJ\),
Hay \(A{\rm{D}} \bot IJ.\)
Copyright © 2021 HOCTAP247
