Bài 44 trang 92 SGK Toán 8 tập 1

Đề bài

Cho hình bình hành \(ABCD\). Gọi  \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\). Chứng minh rằng \(BE = DF\).

Hướng dẫn giải

Áp dụng: +) Tính chất hình bình hành.

+) Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Lời giải chi tiết

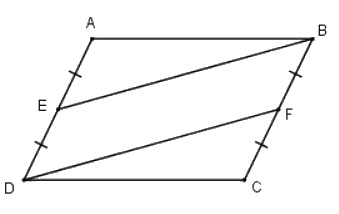
Tứ giác \(BEDF\) có:

\(DE // BF\) (gt) và \(AD=BC\) ( vì \(ABCD\) hình bình hành)

\(E\) là trung điểm của \(AD\) (gt) nên \(DE = \frac{1}{2}AD\) (tính chất trung điểm)

\(F\) là trung điểm của \(BC\) (gt) nên \(BF= \frac{1}{2}BC\) (tính chất trung điểm)

Mà \(AD=BC\) (cmt) nên \(DE=BF\)

Tứ giác \(BEDF\) có \(DE//BF\) (gt) và \(DE=BF\) (cmt)

\( \Rightarrow \) Tứ giác \(BEDF\) là hình bình hành (theo dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(BE = DF\) (tính chất hình bình hành).