Giải bài 45 trang 92 - Sách giáo khoa Toán 8 tập 1

Đề bài

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Vì sao?

Hướng dẫn giải

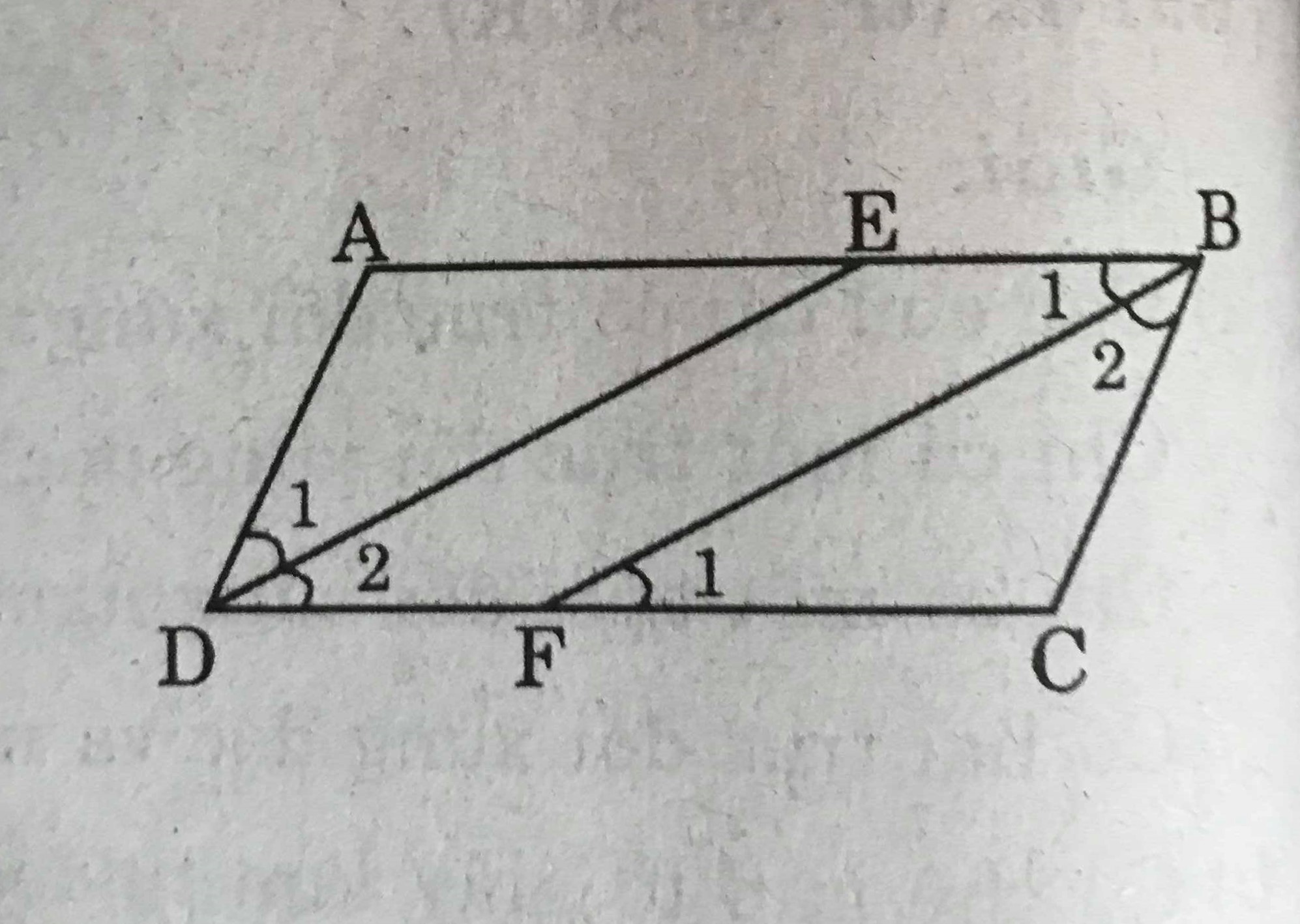
Ta có :  \(\widehat{B_1}=\widehat{D_1}\) (cùng bằng một nửa hai góc bằng nhau \(\widehat{B},\widehat{D}\) )

Ta lại có : AB // CD (ABCD là hình bình hành)

=> \(\widehat{B_1}=\widehat{F_1}\) (so le trong)

Suy ra : \(\widehat{D_1}=\widehat{F_1}\)

Do đó : DE // BF (có hai góc đồng vị bằng nhau)

b) Vì DE // BF và BE // DF nên BEDF là hình bình hành.