Bài 44 trang 133 SGK Toán 8 tập 1

Đề bài

Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO.

Hướng dẫn giải

Áp dụng công thức tính diện tích tam giác.

Lời giải chi tiết

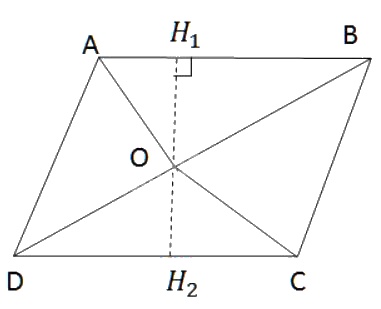
Từ O kẻ đường thẳng d vuông góc với AB ở H₁, cắt CD ở H₂.

Ta có OH₁  ⊥ AB (gt)

Mà AB // CD (gt)

Nên OH₂    ⊥ CD

Do đó  \({S_{ABO}} + {S_{CDO}} \)\(= {1 \over 2}O{H_1}.AB + {1 \over 2}O{H_2}.CD\)

= \({1 \over 2}AB\left( {O{H_1} + O{H_2}} \right)\)

= \({1 \over 2}.AB.{H_1}{H_2}\)

Nên   \({S_{ABO}} + {S_{CDO}} = {1 \over 2}{S_{ABCD}}\) ( 1)

Tương tự  \({S_{BCO}} + {S_{DAO}} = {1 \over 2}{S_{ABCD}}\) (2)

Từ (1) và (2) suy ra :

 \({S_{ABO}} + {S_{CDO}} = {S_{BCO}} + {S_{DAO}}\)