Giải bài 47 trang 133 - Sách giáo khoa Toán 8 tập 1

Đề bài

Vẽ ba đường trung tuyến của một tam giác (h.162). Chứng minh sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau.

Hướng dẫn giải

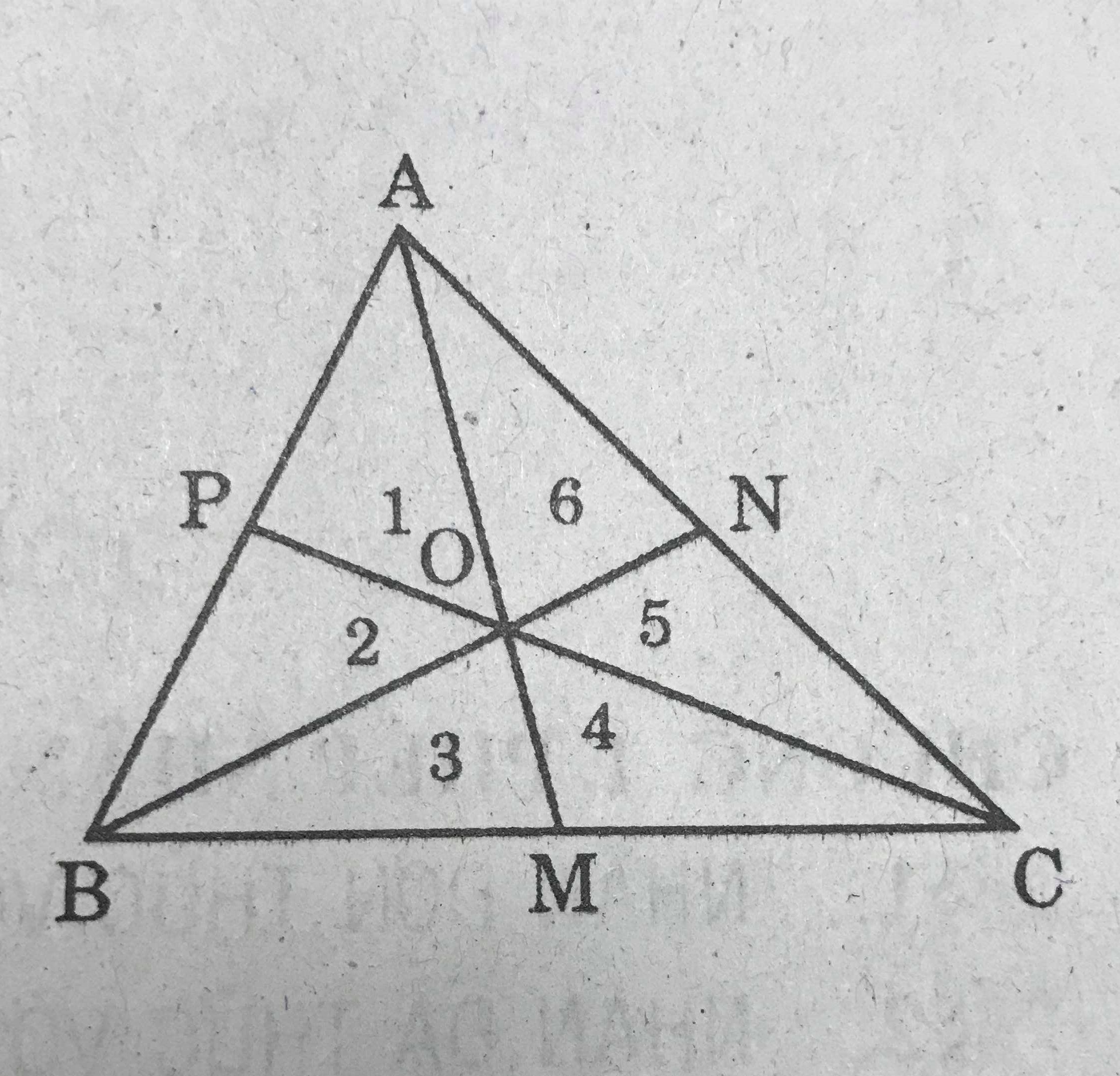
 Ta có : MB = MC và \(\triangle\)BOM và \(\triangle\)COM có chung đường cao kẻ từ O nên :

   \(S_3=S_4=\dfrac{1}{2}S_{BOC}\)

 Lại có : \(S_{BOC}=\dfrac{2}{3}S_{BNC}\)

      và  \(S_{BNC}=\dfrac{1}{2}S_{ABC}\)

Nên \(S_3=S_4=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{1}{2}S_{ABC}=\dfrac{1}{6}S_{ABC}\)

Tương tự : \(S_1=S_2=\dfrac{1}{6}S_{ABC}, S_5=S_6=\dfrac{1}{6}S_{ABC}\)

Do đó : \(S_1=S_2=S_3=S_4=S_5=S_6\)