Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Đại số 9

Đề bài

Bài 1. Tìm tập xác định của mỗi hàm số:

a. \(y = {1 \over {\sqrt {x + 2} }}\)

b. \(y = {1 \over x}\)

Bài 2. Cho hàm số \(y = f\left( x \right) = \sqrt {1 - x} .\) Tính : \(f\left( { - 1} \right);\,f\left( { - 3} \right);\,f\left( 3 \right)\)

Bài 3. Vẽ đồ thị hàm số \(y=-x\)

Hướng dẫn giải

Bài 1. a. \({1 \over {\sqrt {x + 2} }}\) xác định \( \Leftrightarrow \left\{ {\matrix{   {x + 2 \ge 0}  \cr   {x + 2 \ne 0}  \cr  } } \right. \)

\(\Leftrightarrow x + 2 > 0 \Leftrightarrow x >  - 2\)

b. \({1 \over x}\) xác định \( \Leftrightarrow x \ne 0\)

Bài 2. \(\sqrt {1 - x} \) xác định \( \Leftrightarrow 1 - x \ge 0 \Leftrightarrow x \le 1\)

Vậy \(f(3)\) không tồn tại.

Ta có: \(\eqalign{  & f\left( { - 1} \right) = \sqrt {1 - \left( { - 1} \right)}  = \sqrt 2   \cr  & f\left( { - 3} \right) = \sqrt {1 - \left( { - 3} \right)}  = \sqrt 4  = 2 \cr} \)

Bài 3. Bảng giá trị :

       x

       0                 1

       y

       0                -1

       x

       0                 1

       y

       0                -1

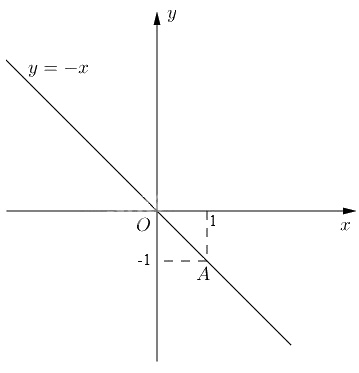
Đồ thị của hàm số \(y = -x\) là đường thẳng qua hai điểm \(O(0; 0)\) và \(A(1; -1)\).