Giải bài 5 trang 45 - Sách giáo khoa Toán 9 tập 1
Tóm tắt bài
Đề bài
a) Vẽ đồ thị của các hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).
b) Đường thẳng song song với trục Ox và cắt trục Oy tại các điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ các điểm A, B, tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimet
Hình 5
Hướng dẫn giải
Hướng dẫn:
Đồ thị hàm số:
y=a.x là một đường thẳng đi qua gốc tọa độ O(0;0) và điểm A(1;a). Nếu điểm M\((x_M;y_M)\) thuộc đường thẳng y=a.x thì tọa độ điểm M thỏa mãn: \(y_M=x.a_M\)
Giải:
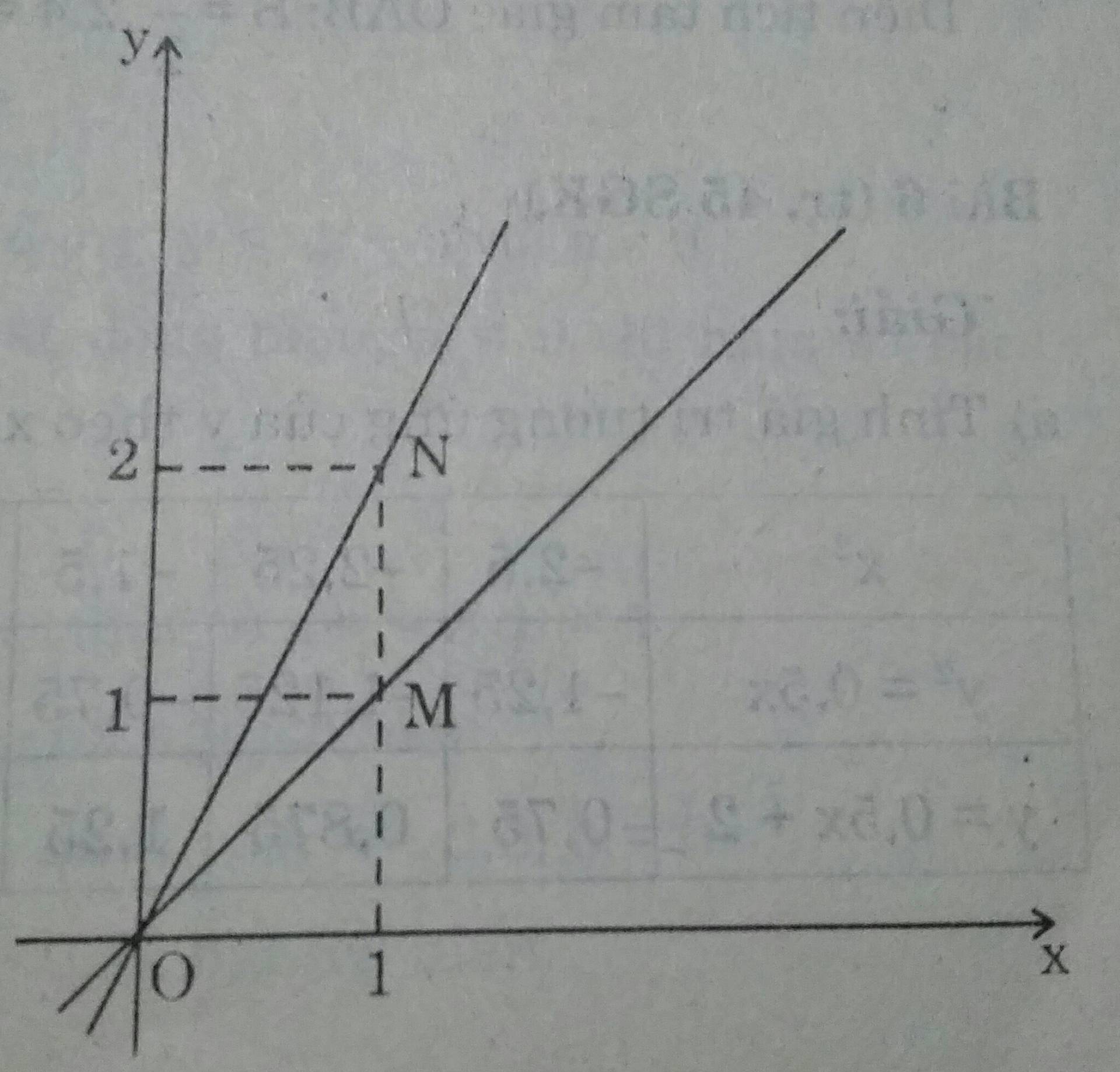
a) Đồ thị hàm số y= ax đi qua O(0;0) và M(1;1)
Đồ thị hàm số y=2x đi qua O(0;0) và N(1;2)
b)
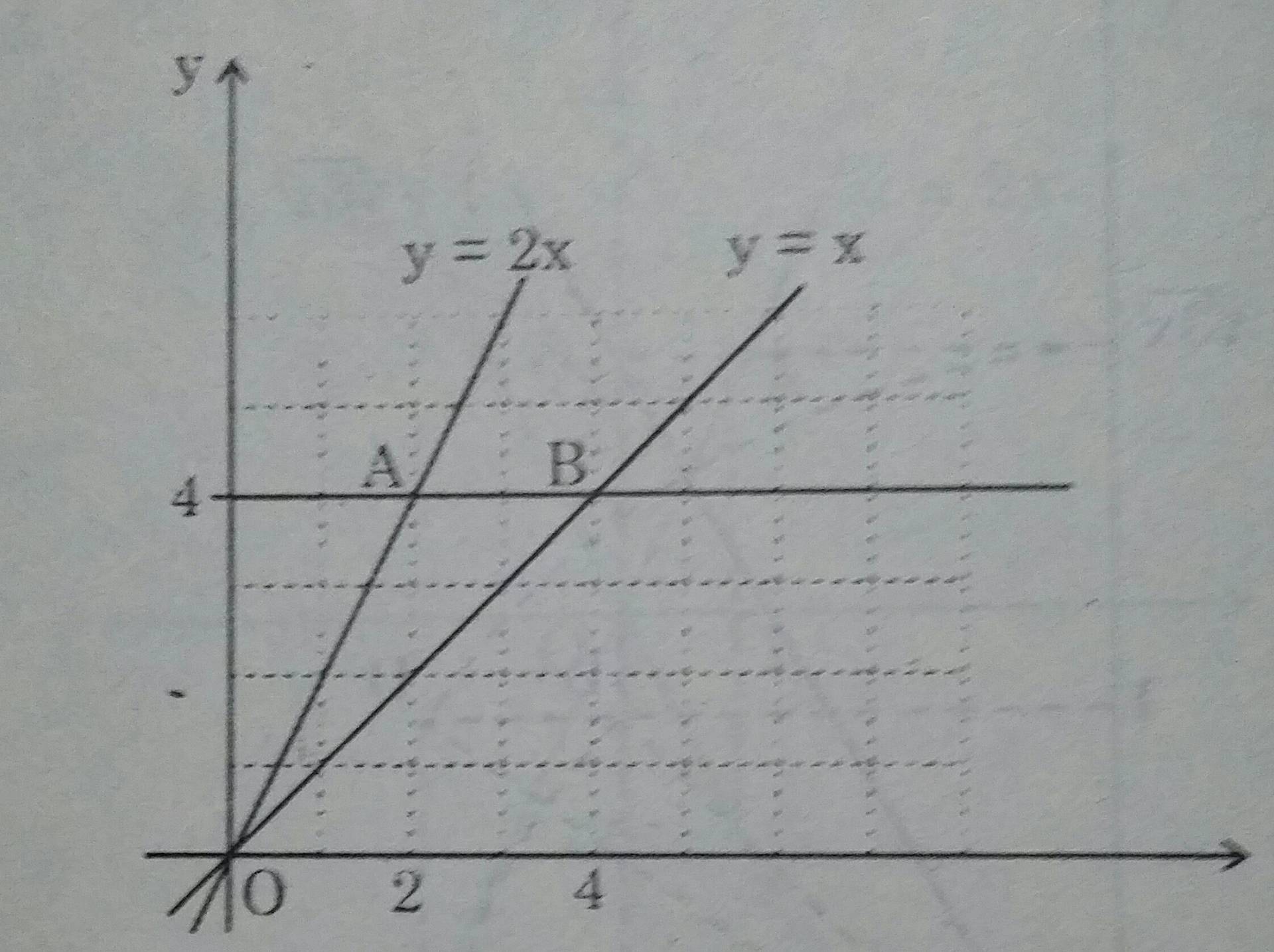
- Tọa độ điểm A: cho y=4 thì 2x=4 nên x=2, ta có A(2;4).
- Tọa độ điểm B: cho y =4 thì x=4, ta có B(4,4).
- Tính chu vi, diện tích tam giác OAB:
từ hình vẽ ta có: AB=4-2= 2(cm)
Áp dụng định lý Py-ta-go:
OA= \( \sqrt{2^2+4^2}= 2\sqrt{5}\) (cm)
OB= \(\sqrt{4^2}+\sqrt{4}=4\sqrt{2}\) (cm)
Chu vi tam giác OAB: P= \( 2+ 2\sqrt{5}+4\sqrt{2} \approx 12,13(cm)\)
Diện tích tam giác OAB: S= \( \frac{1}{2}.2.4=4(cm^2)\)
Copyright © 2021 HOCTAP247
