Đề kiểm 15 phút - Đề số 3 - Bài 8 - Chương 3 - Hình học 9
Tóm tắt bài
Đề bài
Cho tam giác đều ngoại tiếp đường tròn (I; r = 2cm).
a) Tính cạnh của tam giác đều.
b) Tính bán kính của đường tròn ngoại tiếp tam giác đó.
Hướng dẫn giải
a)
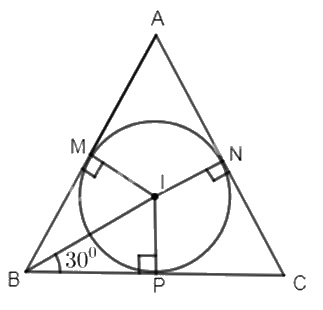
Ta có BM, BP là hai tiếp tuyến với đường tròn (I; r) nên BI là phân giác của \(\widehat {ABC}\)
\( \Rightarrow \widehat {IBP} = 30^\circ \).
Xét tam giác vuông IBP, ta có :
\(BP = IP.\cot 30^\circ = r\sqrt 3 \)
Do đó : \(BC = 2r\sqrt 3 = 4\sqrt 3 \) cm
Vậy cạnh của tam giác đều ngoại tiếp đường tròn (I; r = 2cm) là \(4\sqrt 3 \) cm.
b) ∆IBP vuông tại P có \(\widehat {IBP} = 30^\circ \) nên \(BI = 2IP = 2r = 2.2 = 4\) (cm)
Tương tự ta tính được \(AI = CI = 4\) (cm)
\( \Rightarrow AI = BI = CI = 4\) (cm) nên I chính là tâm của đường tròn ngoại tiếp ∆ABC.
Do đó bán kính của đường tròn ngoại tiếp ∆ABC là 4 (cm).
Copyright © 2021 HOCTAP247
