Giải bài 64 trang 92 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho

   a) Tứ giác ABCD là hình gì?

   b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.

   c) Tính độ dài các cạnh của tứ giác ABCD theo R.

Hướng dẫn giải

   

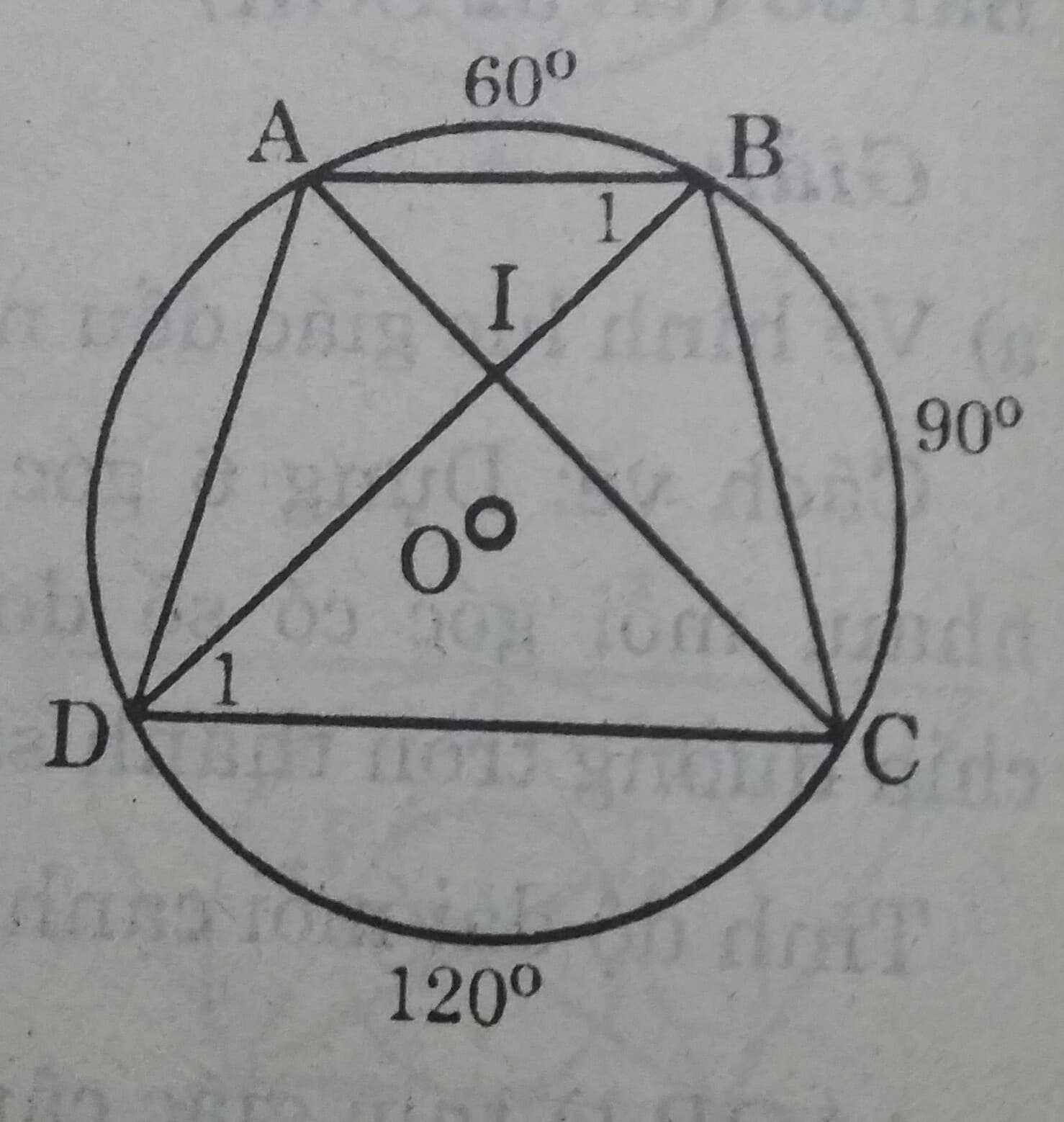
   a)

    \(sđ \stackrel\frown{AD}= 360^0 - ( 60^0 + 90^0 + 120^0)= 90^0\\ Vậy \stackrel\frown{CD} = \stackrel\frown{BC} \Rightarrow \stackrel\frown{AD} =\stackrel\frown{BC}\\ Ta\ có \ \widehat{B_1}=\widehat{D_1}\)

  Suy ra AB// CD.

   Do đó tứ giác ABCD là hình thang.

   Hình thang ABCD nội tiếp đường tròn (O) nên nó là hình thang cân.

    b) Gọi \(I\) là giao điểm của hai đường chéo.

    \(\widehat{BIC}\) là góc có đỉnh ở bên đường tròn nên

    \(\widehat{BIC}=\dfrac{ sđ \stackrel\frown{AD}+sđ \stackrel\frown{BC}}{2}= \dfrac{90^0+ 90^0 }{2}= 90^0\\ Vậy AC \perp BD\)

    c) \(sđ \stackrel\frown{AB} = 60^0 \) nên AB là cạnh của một lục giác đều nội tiếp, do đó AB = R.

    Vì \(sđ \stackrel\frown{BC}= sđ \stackrel\frown{AD}=90^0\) nên BC và AD là các cạnh của một hình vuông nội tiếp, đo đó BC = AD = \(R\sqrt{2}\)

    Vì \(sđ \stackrel\frown{CD} = 120^0 \) nên CD là cạnh của một tam giác đều nội tiếp, do đó CD= \(R\sqrt{3}\)