Giải bài 62 trang 91 - Sách giáo khoa Toán 9 tập 2

Đề bài

    a) Vẽ tam giác đều ABC cạnh a = 3cm.

    b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.

Hướng dẫn giải

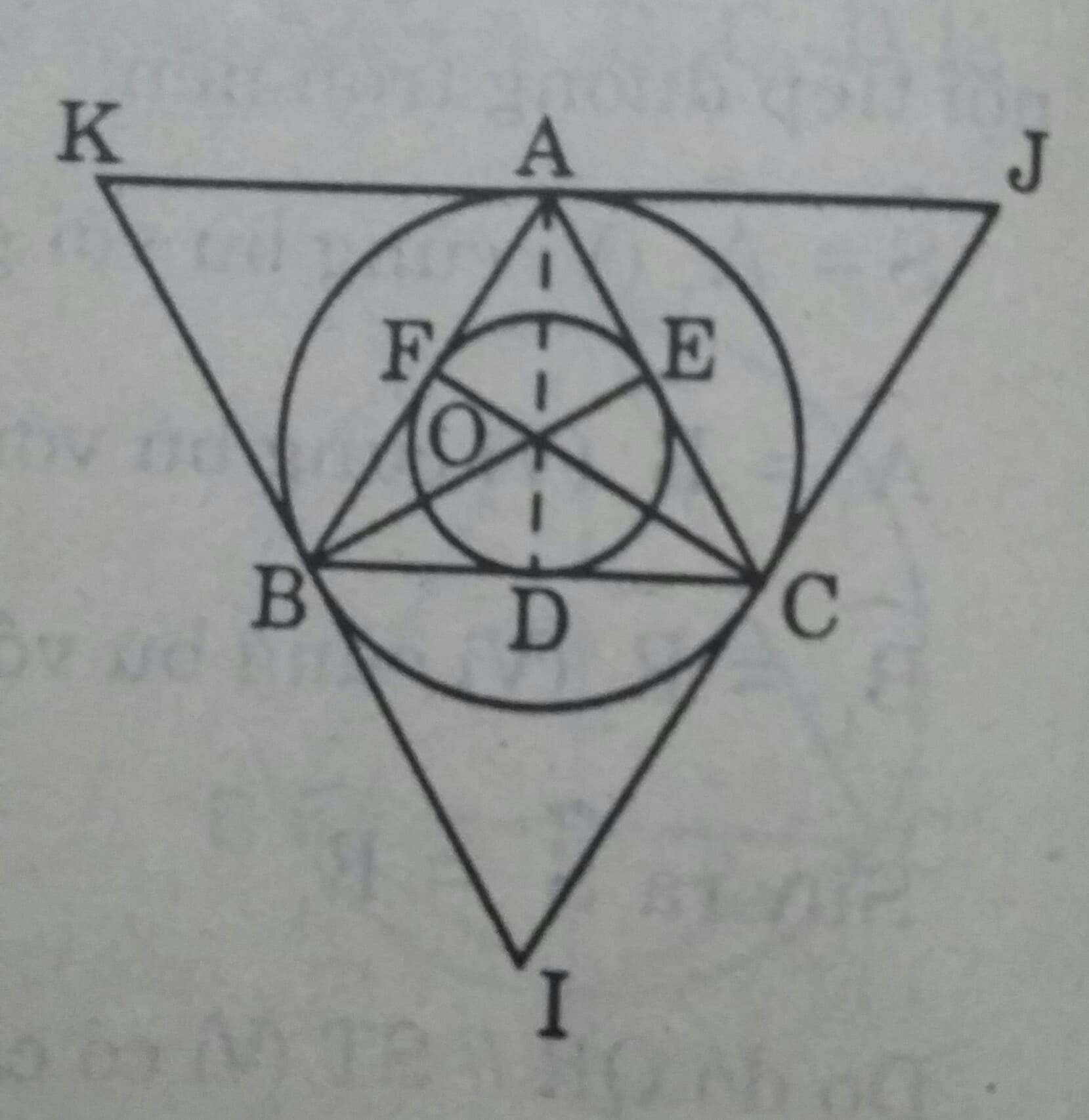
   a) Vẽ tam giác đều ABC, cạnh BC= a= 3cm.

   b) Vẽ các đường trung trực của các cạnh chúng gặp nhau tạo O, đó là tâm đường tròn ngoại tiếp, nội tiếp tam giác ABC.

  Vẽ đường tròn (O; OA) ta được đường tròn ngoại tiếp tam giác đều.

   Ta có \(R= OA = \dfrac{2}{3}AD= \dfrac{2}{3}. \dfrac{3\sqrt{3}}{2}= \sqrt{3}(cm)\)

   c) Vẽ đường tròn (O; OD) ta được đường tròn nội tiếp tam giác đều.

   Ta có \(r= OD = \dfrac{1}{3}AD= \dfrac{1}{3}. \dfrac{3\sqrt{3}}{2}= \dfrac{\sqrt{3}}{3}(cm)\)

  d) Vẽ các tiếp tuyến của đường tròn (O;R) tại A, B,C. Ba tiếp tuyến này cắt nhau tại \(I,J,K\). Tam giác \(IJK\) là tam giác đều ngoại tiếp đường tròn (O,R).