Bài 96 trang 105 SGK Toán 9 tập 2

Đề bài

Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\) và tia phân giác của góc \(A\) cắt đường tròn tại \(M\). Vẽ đường cao \(AH\). Chứng minh rằng:

a) \(OM\) đi qua trung điểm của dây \(BC\).

b) \(AM\) là tia phân giác của góc \(OAH\).

Hướng dẫn giải

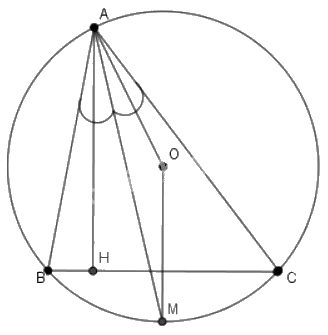
a) Vì \(AM\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAM} = \widehat {MAC}\)  

Mà \(\widehat {BAM}\) và \(\widehat {MAC}\) đều là góc nội tiếp của \((O)\) nên 

\(\overparen{BM}\)=\(\overparen{MC}\)

⇒ \(M\) là điểm chính giữa cung \(BC\)

Vậy \(OM \bot BC\) và \(OM\) đi qua trung điểm của \(BC\)

b) Ta có : \(OM \bot BC\) và \(AH\bot BC\) nên \(AH//OM\)

\( \Rightarrow \widehat {HAM} = \widehat {AM{\rm{O}}}\)  (so le trong)  (1)

Mà \(∆OAM\) cân tại \(O\) nên \(\widehat {AM{\rm{O}}} = \widehat {MAO}\)  (2)

Từ (1) và (2) suy ra: \(\widehat {HA{\rm{M}}} = \widehat {MAO}\) 

Vậy \(AM\) là đường phân giác của góc \(OAH\)