Cách xác định giá trị lượng giác của một cung Hình học

Cách xác định giá trị lượng giác của một cung Hình học

Định nghĩa cung trong Hình học là gì? Để xác định giá trị lượng giác của cung bạn cần làm như thế nào? Câu hỏi sẽ được giải đáp trong bài giảng dưới đây. Mời các bạn cùng theo dõi!

I. Định nghĩa

    1. Cung trong hình học là gì?

Được định nghĩa là một phần của đường tròn hay, là một phần của chu vi (biên) của hình tròn, đoạn đóng của một đường cong khả vi trong một đa tạp.

Một cung tròn thường được cấu tạo bởi dây cung, bán kinh dây cung và góc tạo bởi hai bán kính.

Cung được ký hiệu: ⌒

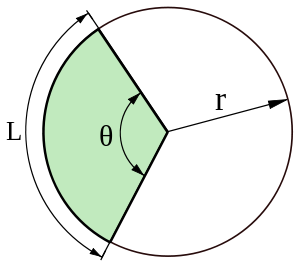
Nhận thấy cung tròn được tạo bởi dây cung L, bán kinh dây cung là r.

Công thức liên quan:

• Bài 4. Phép thử và biến cố

• Bài 5. Xác suất và biến cố

    2. Xác định giá trị lượng giác của cung

Các công thức liên quan đến cung hình học thường là công thức tính độ dài dây cung, xác định góc của hình cung, bán kinh cung tròn. Trong đó, công thức quan trọng nhất mà bạn thường gặp trong để thi đó chính là công thức tính diện tích giới hạn cung tròn và tâm đường tròn.

Diện tích phần giới hạn bởi cung tròn và tâm đường tròn:

\({\displaystyle A={\frac {1}{2}}r^{2}\theta .}\)

Chia hai vế cho \({\displaystyle {\pi r^{2}}}\)

Tỷ lệ giữa diện tích A và diện tích phần giới hạn trong đường tròn bằng với tỷ lệ giữa số đo góc \({\displaystyle \theta }\) và số đo góc cả đường tròn

\({\displaystyle {\frac {A}{\pi r^{2}}}={\frac {\theta }{2\pi }}.}\)

Giản lược \({\displaystyle \pi }\) ở cả hai vế

\({\displaystyle {\frac {A}{r^{2}}}={\frac {\theta }{2}}.}\)

Nhân hai vế với \({\displaystyle r^{2}}\), thu được

\({\displaystyle A={\frac {1}{2}}r^{2}\theta .}\)

Tương tự phần trên, công thức tương đương nếu số đo góc đo bằng độ:

\({\displaystyle A={\frac {\alpha }{360}}\pi r^{2}.}\)

• Bảng xác định dấu của các giá trị lượng giác

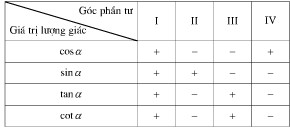
• Các công thức hệ quả liên quan:

 \(sin^2 a+cos^2 a=1, \forall a\)

\(1+ tan^2a=\dfrac{1}{cos^2}, a\neq \dfrac{\pi}{2}+k\pi, k\in Z\)

\(1+ cot^2a=\dfrac{1}{sin^2}, a\neq k\pi, k\in Z\)

\(tan a.cot a= 1, a\neq \dfrac{\pi}{2},k \in Z\)

II. Bài tập trắc nghiệm giá trị lượng giác của một cung

Xem thêm: Bài 2. Giá trị lượng giác của cung

Hy vọng thông qua bài học trên, bạn đọc có thể hiểu rõ hơn và nắm chắc cách giải dạng bài tập giá trị lượng giác của một cung. chúc bạn có những giờ học vui vẻ!