Trọn bộ kiến thức giá trị lượng giác của một cung

Trong chương trình toán học lớp 10 thì giá trị lượng giác của một cung được coi như là kiến thức hết sức quan trọng, tạo tiền đề cho những bài học phía sau. Vậy nên hãy cùng với đi tìm hiểu giá trị lượng giác của một cung (hay góc lượng giác), bảng giá trị lượng giác ngay thôi.

I) Định nghĩa

Cho một nửa đường tròn đơn vị tâm O, trên nửa đường tòn lấy điểm M(a, b). Ta xét góc nhọn \(\alpha = \widehat{aOM}\)

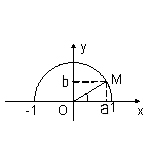
- \(sin \alpha = y\)

- \(cos \alpha = x\)

- \(tan \alpha = \dfrac {y}{x} (x\neq 0)\)

- \(cot \alpha = \dfrac {x}{y} (y\neq 0)\)

♦ Chú ý:

• \(tan \alpha\) xác định khi \(\alpha \neq 90^0\)
• \(cot \alpha \) xác định khi \(\alpha \neq 0^0\) và \(\alpha \neq 180^0\)

II) Hệ quả giá trị lượng giác của góc lượng giác

1) Hệ quả 1

 \(-1 \leq sin \alpha \leq 1, -1 \leq cos \alpha \leq 1\) với mọi \(\alpha \in \mathbb{R}\)

\(sin (\alpha + k2\pi) = sin \alpha (k\in Z)\)

\(cos (\alpha + k2\pi) = cos \alpha (k\in Z)\)

2) Hệ quả 2

 \(tan \alpha\) xác định với mọi  \(\alpha \neq \dfrac {\pi}{2} + k\pi, k \in Z\)

     \(cot \alpha\) xác định với mọi  \(\alpha \neq k\pi, k \in Z\)

\(tan \alpha = tan (\alpha + k\pi), k\in Z\)

\(cot\alpha = cot (\alpha + k\pi), k\in Z\)

3) Bảng xác định dấu các giá trị lượng giác

4) Hệ thức lượng cơ bản

a)  \(sin^2\alpha + cos^2\alpha = 1\)

b)  \(tan\alpha.cot\alpha = 1\)

c)  \(1 + cot^2\alpha = \dfrac {1}{sin^2\alpha}\)

d)  \(1 + tan ^2\alpha = \dfrac {1}{cos^2\alpha}\)

III) Tính chất giá trị lượng giác của góc lượng giác

1) Góc phụ nhau

a) \(cos\alpha =sin (90^0 - \alpha)\)

b) \(sin \alpha =cos (90^0 - \alpha)\)

c) \(cot \alpha = tan (90^0 - \alpha)\)

d) \(tan \alpha = cot (90^0 - \alpha)\)

2) Góc bù nhau

a) \(sin\alpha = sin(180^0 - \alpha)\)

b) \(- cos \alpha = cos (180^0 - \alpha)\)

c) \(-tan \alpha = tan (180^0 - \alpha)\)

d) \(-cot \alpha = cot (90^0 - \alpha)\)

3) Góc đối nhau

a) \(cos(-\alpha) = cos\alpha\)

b) \(sin (-\alpha) = -sin \alpha\)

c) \(tan (-\alpha) = -tan \alpha\)

d) \(cot (-\alpha) = -cot \alpha\)

4) Góc hơn kém \(\pi\)

a) \(cos (\pi + \alpha) = -cos\alpha\)

b) \(sin (\pi + \alpha) = sin\alpha\)

c) \(tan (\pi - \alpha) = tan\alpha\)

d) \(cot(\pi + \alpha) = cot \alpha\)

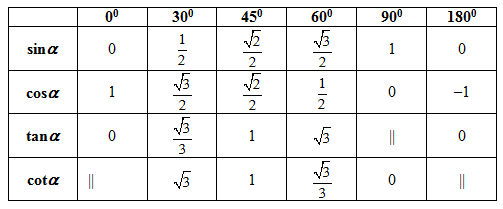
Dưới đây gửi đến các bạn bảng lượng giác đầy đủ về các góc lượng giác đặc biệt.

(bảng giá trị lượng giác cung đặc biệt)

IV) Luyện tập

Bài 1: Tính \(sin 15^0, cos 15^0, cot 15^0\), biết rằng \(tan 15^0 = 2 - \sqrt{3}\)

Bài 2: Hãy rút gọn các biểu thức dưới đây

a) \(\dfrac{tan \alpha}{sin \alpha}- \dfrac {sin\alpha}{cot\alpha}\)

b) \(cos^2\dfrac{a}{3} + cot^2{a}{3} - \dfrac {1}{sin^2\dfrac{a}{3}}\)

Bài 3: Tính giá trị biểu thức \(C = \dfrac {2tan\alpha +cot\alpha}{tan\alpha - cot\alpha}\). Biết rằng \(cos \alpha = \dfrac {4}{5}\)

Xem thêm>>> Hướng dẫn bài tập SGK

                        Bài 3. Công thức lượng giác

Trên đây là những kiến thức lý thuyết và bài tập mà đã tổng hợp được về giá trị lượng giác của góc lượng giác. Để lại đáp án bài tập và ý kiến thắc mắc của bản thân ở phía dưới comment nhé!