Bài 3 trang 17 SGK Hình học 10
Tóm tắt bài
Đề bài
Trên đường thẳng chứa cạnh \(BC\) của tam giác \(ABC\) lấy một điểm \(M\) sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} \). Hãy phân tích vectơ \(\overrightarrow {AM} \) theo hai vectơ \(\overrightarrow u = \overrightarrow {AB} ;\overrightarrow v = \overrightarrow {AC}. \)
Hướng dẫn giải
+) Với 3 điểm \(A, \, \, B, \, \, C\) bất kì ta luôn có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} .\)
Lời giải chi tiết
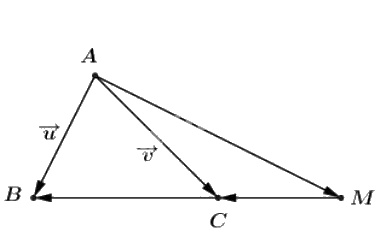
Trước hết ta có
\(\eqalign{
& \overrightarrow {MB} = 3\overrightarrow {MC}\cr& \Rightarrow \overrightarrow {MB} = 3.(\overrightarrow {MB} + \overrightarrow {BC} ) \cr
& \Rightarrow \overrightarrow {MB} = 3\overrightarrow {MB} + 3\overrightarrow {BC} \cr
& \Rightarrow - 2\overrightarrow {MB} = 3\overrightarrow {BC} \cr
& \Rightarrow \overrightarrow {BM} = {3 \over 2}\overrightarrow {BC} \cr} \)
mà \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) nên \(\overrightarrow {BM} = {3 \over 2}(\overrightarrow {AC} - \overrightarrow {AB} )\)
Theo quy tắc \(3\) điểm, ta có
\(\eqalign{
& \overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \cr&\;\;\;\;\;\;\;\;= \overrightarrow {AB} + {3 \over 2}(\overrightarrow {AC} - \overrightarrow {AB} ) \cr&\;\;\;\;\;\;\;\;\;= - {1 \over 2}\overrightarrow {AB} + {3 \over 2}\overrightarrow {AC} \cr
&\text{ Hay } \overrightarrow {AM} = - {1 \over 2}\overrightarrow u + {3 \over 2}\overrightarrow v \cr} \)
Copyright © 2021 HOCTAP247
