Bài 9 trang 17 SGK Hình học 10
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác đều \(ABC\) có trọng tâm \(O\) và \(M\) là một điểm tùy ý trong tam giác. Gọi \(D,E,F\) lần lượt là chân đường vuông góc hạ từ \(M\) đến \(BC, AC, AB\). Chứng minh rằng:
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = {3 \over 2}\overrightarrow {MO} \)
Hướng dẫn giải
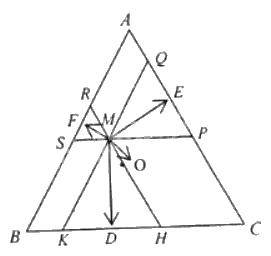
Qua M kẻ các đường thẳng song song với các cạnh của tam giác
A1B1 // AB; A2C2 // AC; B2C1 // BC.
Dễ thấy các tam giác MB1C2; MA1C1;MA2B2 đều là các tam giác đều. Ta lại có MD 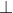 B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
Ta có 2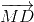 =
=  +
+ 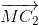
Tương tự: 2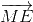 =
= 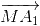 +
+ 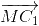
2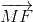 =
= 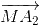 +
+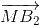
=> 2( 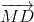 +
+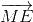 +
+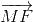 ) = (
) = (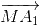 +
+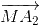 ) + (
) + (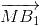 +
+ 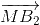 ) + (
) + (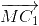 +
+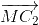 )
)
Tứ giác là hình bình hành nên
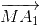 +
+ 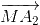 =
= 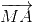
Tương tự: 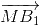 +
+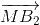 =
= 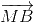
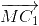 +
+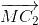 =
= 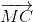
=> 2( 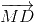 +
+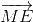 +
+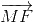 ) =
) = 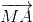 +
+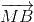 +
+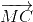
vì O là trọng tâm bất kì của tam giác và M là một điểm bất kì nên
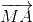 +
+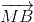 +
+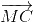 = 3
= 3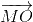 .
.
Cuối cùng ta có:
2( 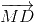 +
+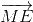 +
+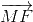 ) = 3
) = 3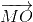 ;
;
=> 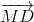 +
+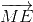 +
+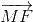 =
= 
Copyright © 2021 HOCTAP247
