Bài 5 trang 17 SGK Hình học 10
Tóm tắt bài
Đề bài
Gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\) của tứ giác \(ABCD\). Chứng minh rằng:
\(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Hướng dẫn giải
Với \(M\) là trung điểm của \(AB\) ta có:
+) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)
+) Với mọi điểm \(O\) bất kì ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} .\)
Lời giải chi tiết
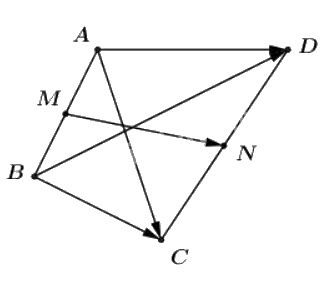
\(N\) là trung điểm của \(CD\) nên ta có:
\(2\overrightarrow {MN} = \overrightarrow {MC} + \overrightarrow {MD} \) (1)
Theo quy tắc 3 điểm, ta có:
\(\overrightarrow {MC} = \overrightarrow {MA} + \overrightarrow {AC} \) (2)
\(\overrightarrow {MD} = \overrightarrow {MB} + \overrightarrow {BD} \) (3)
Từ (1), (2), (3) ta có:
\(2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {MB} + \overrightarrow {BD} \)
\(= \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \overrightarrow {AC} + \overrightarrow {BD} \)\( = \overrightarrow {AC} + \overrightarrow {BD} \)
Chứng minh tương tự, ta có: \(2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD}. \)
Copyright © 2021 HOCTAP247
