Bài 4 trang 17 SGK Hình học 10
Tóm tắt bài
Đề bài
Gọi \(AM\) là trung tuyến của tam giác \(ABC\) và \(D\) là trung điểm của đạn \(AM\). Chứng minh rằng:
a) \(2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \)
b) \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \), với \(O\) là điểm tùy ý.
Hướng dẫn giải
Với \(M\) là trung điểm của \(AB\) ta có:
+) \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 .\)
+) Với mọi điểm \(O\) bất kì ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} .\)
Lời giải chi tiết
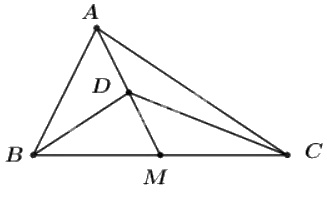
a) Vì \(M\) là trung điểm của \(BC\) nên:
Ta có:
\(\overrightarrow {DB} + \overrightarrow {DC} = 2\overrightarrow {DM} \)
Mặt khác, do \(D\) là trung điểm của đoạn \(AM\) nên \(\overrightarrow {DM} = - \overrightarrow {DA} \)
Khi đó: \(2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 2\overrightarrow {DA} + 2\overrightarrow {DM} \)\(= 2\left( {\overrightarrow {DA} + \overrightarrow {DM} } \right) = \overrightarrow 0 \)
b) Ta có:
\(\eqalign{
& 2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \cr
& \Leftrightarrow 2\left( {\overrightarrow {OA} - \overrightarrow {OD} } \right) + \left( {\overrightarrow {OB} - \overrightarrow {OD} } \right) \cr&+ \left( {\overrightarrow {OC} - \overrightarrow {OD} } \right) = \overrightarrow 0 \cr
& \Leftrightarrow 2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \cr} \) (Đúng theo câu a)
Vậy: \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \), với \(O\) là điểm tùy ý
Copyright © 2021 HOCTAP247
