Bài 4 trang 45 SGK Hình học 10
Tóm tắt bài
Đề bài
Trên mặt phẳng \(Oxy\), cho hai điểm \(A(1; 3), \, B(4;2)\)
a) Tìm tọa độ điểm \(D\) nằm trên trục \(Ox\) sao cho \(DA = DB\);
b) Tính chu vi tam giác \(OAB\);
c) Chứng tỏ rằng \(OA\) vuông góc với \(AB\) và từ đó tính diện tích tam giác \(OAB.\)
Hướng dẫn giải
+) Điểm \(D \in Ox \Rightarrow D(x_0; \, 0).\)
\(\begin{array}{l}
+ )\;\;DA = DB \Leftrightarrow D{A^2} = D{B^2}\\
\Leftrightarrow {\left( {{x_A} - {x_D}} \right)^2} + {\left( {{y_D} - {y_A}} \right)^2} \\= {\left( {{x_B} - {x_D}} \right)^2} + {\left( {{y_B} - {y_D}} \right)^2}.
\end{array}\)
+) Chu vi tam giác \(OAB:\;\;\;C = OA + OB + AB.\)
+) \(OA \bot AB \Leftrightarrow \overrightarrow {OA} .\overrightarrow {AB} = 0.\)
\( \Rightarrow {S_{OAB}} = \frac{1}{2}OA.AB.\)
Lời giải chi tiết
a) \(D\) nằm trên trục \(Ox\) nên tọa độ của \(D\) là \((x; 0)\).
Ta có : \(\overrightarrow {DA} = \left( {1 - x;\;\;3} \right),\;\;\overrightarrow {DB} = \left( {4 - x;\;2} \right).\)
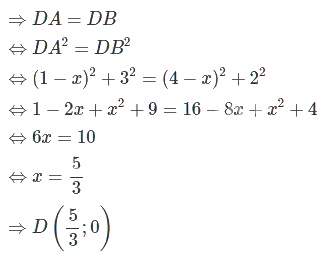
\(\eqalign{b) & O{A^2} = {1^2} + {3^3} = 10 \Rightarrow OA = \sqrt {10} \cr & O{B^2} = {4^2} + {2^2} = 20 \Rightarrow OB = 2\sqrt 5 \cr & A{B^2} = {(4 - 1)^2} + {(2 - 3)^2} = 10 \cr&\Rightarrow AB = \sqrt {10} \cr} \)
Chu vi tam giác \(OAB\) là: \(\sqrt {10} + 2\sqrt 5 + \sqrt {10}=2\sqrt {10} + 2\sqrt 5. \)
c) Ta có \(\vec{OA}= (1; 3)\)
\(\vec{AB} = (3; -1)\)
\(\vec{OA} .\vec{AB} = 1.3 + 3.(-1) = 0 \Rightarrow \vec{OA}\) ⊥ \(\vec{AB}\)
\({S_{OAB}}=\frac{1}{2}|\vec{OA}| .|\vec{AB}| =\frac{1}{2}.\sqrt{10}.\sqrt{10}\)\( =5\) (đvdt)
Copyright © 2021 HOCTAP247
